عدد نپر

[faridrajaee1]

با سلام لطفا اگر در مورد روش پیدا کردن خود عدد نپر و اینکه از کجا آمده اطلاعاتی دارید توضیح دهید با تشکر

[Mehran-King]

با سلام لطفا اگر در مورد روش پیدا کردن خود عدد نپر و اینکه از کجا آمده اطلاعاتی دارید توضیح دهید با تشکر

e یک عدد حقیقی یکتاست، به طوری که مقدار مشتق تابع در نقطهٔ برابر شود.^[۱] از این طریق تابع به عنوان تابع نمایی و تابع معکوس آن، به عنوان تابع لگاریتم طبیعی یا لگاریتم در مبنای معرفی می‌شود. از طرفی می‌توان را به عنوان مبنای تابع لگاریتم طبیعی(با استفاده از انتگرال)، به عنوان حد یک دنباله ریاضی و یا به عنوان حد یک سری ریاضی تعریف کرد. گاهی عدد ، به افتخار ریاضی‌دان سوئیسی، لئونارد اویلر (به آلمانی: Leonhard Euler)‏، عدد اویلر نامیده می‌شود. همچنین گاهی نیز از آن به اسم ثابت نپر (جان نپر (به انگلیسی: John Napier)‏) یاد می‌شود، با این حال نماد به افتخار اویلر انتخاب شده‌است.
در ریاضیات عدد در کنار عدد ۰، عدد ۱، عدد پی (به یونانی: π)‏(همون پی خودمون) و عدد یکه موهومی از معروفیت خاصی در ریاضی برخوردار است.^[۲] علاوه بر تعریف انتزاعی آن‌ها، این پنج عدد نقش مهم و کلیدیی در سرتاسر ریاضیات بازی می‌کنند. برای مثال می‌توان هر پنج عدد را در معادلهٔ مشخصهٔ اویلر^[۳] مشاهده کرد.

عدد یک عدد گنگ است؛ یعنی این عدد، کسری از اعداد صحیح نیست. به علاوه، این عدد یک عدد متعالی است؛ یعنی نمی‌تواند ریشهٔ هیچ معادلهٔ چند جمله‌ای غیر صفر با ضرایب حقیقی باشد. عدد تا ۵۰ رقم اعشار مطابق عدد زیر است:
۲٫۷۱۸۲۸۱۸۲۸۴۵۹۰۴۵۲۳۵۳۶۰۲۸ ۷۴۷۱۳۵۲۶۶۲۴۹۷۷۵۷۲۴۷۰۹۳۶۹۹ ۹۵...^[۴]

e یک عدد حقیقی مانند است، به طوری که مقدار مشتق تابع (منحنی آبی) در نقطهٔ برابر شود. برای مقایسه، در شکل تابع (منحنی نقطه چین) و تابع (منحنی خط چین) مشاهده می‌شود. خط قرمز، خطی با شیب یک است که از نقطهٔ می‌گذرد.

عدد e مهمترین عدد در ریاضیات است كه به نام عدد اویلر یا عدد نپر Napier نیز نامیده می شود و تقریبا برابر است با 2.7182818284590452353602874713527 كه البته بیش از 100 میلیارد رقم بعد از اعشار آن نیز حساب شده است. این عدد به چند طریق بدست می آید و یكی از فرمولهای محاسبه اش

e = (1 + 1/n)n
است هنگامی كه n به سمت بینهایت میل كند

n (1 + 1/n)n 1 2.00000 2 2.25000 5 2.48832 10 2.59374 100 2.70481 1,000 2.71692 10,000 2.71815 100,000 2.71827

برخی دانشجویان تا 9 رقم بعد از اعشارش را بخاطر می سپارند چون آسان است:

2.7 1828 1828
و برخی افراد شش رقم بعد را هم با این رابطه حفظ می كنند كه یك مثلث متساوی الساقین قائم الزاویه زوایایش بترتیب 45 و 90 و 45 درجه است
2.7 1828 1828 45 90 45
فرمول دوم برای محاسبه عدد اویلر وتوانهای آن بشرح زیر است::



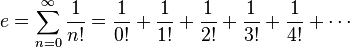
منبع : ویکی پدیا-تبیان