سلام
لطفا اين دو تمرين رو ثابت كنيد
بعد از بسط دادن هست ...
و
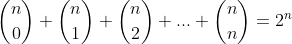

سلام
لطفا اين دو تمرين رو ثابت كنيد
بعد از بسط دادن هست ...
و
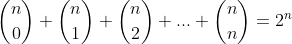
من اولي رو بلد نيستم
ولي در مورد دومي اينو ميدونم که مجموع تعداد زيرمجموعه هاي يک مجموعه n عضوي از 2 به توان n بدست مياد.(طرف دوم رابطه ی شما)
از طرفي تعداد زيرمجموعه هاي يک عضوي همون مجموعه از(c (n,1 و تعداد زيرمجموعه هاي دو عضوي از( c (n,2 و ...
طرف اول رابطه ي شما مجموع تعداد زير مجموعه ها هست که با طرف دوم برابر هست.
سلام.
سوال اولتون فقط برای n ها فرد درسته و در مورد n ها زوج صدق نمیکنه. (مثال نقض خیلی ساده اش n=0 یا n=2 ) هستش.
برای اثبات سوال اول در حالت n های فرد هم باید به این نکته دقت کنین که در ترکیب داریم:
( چرا؟ )
بنابراین جملات از ابتدا و انتها یکی یکی با هم خنثی میشن و حاصل نهایی برابر با صفره.
----------------------------------------------
برای حل سوال دوم، ابتدا خودمون میایم و یک مساله طرح میکنیم که به درک بهتر از مساله شما کمک میکنه و اون سوال اینه:
به چند روش میشه از یک مجموعه با n عضو متمایز، یک زیر مجموعه درست کرد؟
حالا این مساله رو به دو روش حلش میکنیم:
* روش اول :
زیر مجموعه ای که میخواهیم بسازیم:
الف) ممکنه تهی باشه
ب) ممکنه فقط یه عضو داشته باشه که در اون صورت برای درست کردن یک زیر مجموعه ی یک عضوی از مجموعه ای n عضوی،تا انتخاب داریم.
ج) ممکنه زیر مجموعه دو عضوی باشه. بنابراین باید دو عضو از مجموعه ی مرجع رو انتخاب کنیم که تعداد کل حالات میشه:
.
.
.
؟؟؟ ) ممکنه زیر مجموعه ی ما دقیقا برابر با خود مجموعه ی مرجع باشه. بنابراین باید همه ی اعضای مجموعه ی مرجع رو برای زیر مجموعه ی مورد نظرمون انتخاب کنیم:
حالا حاصل کل برابر با مجموع تعداد زیر مجموعه هاییه که تا اینجا محاسبه کردیم:
* روش دوم :
فرض کنین که میخوایم یک زیر مجموعه ی دلخواه از مجموعه ی n عضوی مرجعمون داشته باشیم. خب توی این زیر مجموعه، عضو اول مجموعه ی مرجع میتونه باشه و میتونه هم نباشه. پس برای عضو شماره ی یک از مجموعه ی مرجع، 2 حالت داریم. برای عضو دوم از مجموعه ی مرجع هم همین حالت برقراره، یعنی میتونه در زیرمجموعه ی دلخواه ما باشه و میتونه هم نباشه. بنابراین برای عضو شماره دو هم 2 حالت داریم. برای همه ی اعضاء مجموعه ی مرجع همین استدلال برقراره و برای حضور یا عدم حضور هر یک از اونها 2 حالت وجود داره. و چون حضور یا عدم حضور هر یک از اعضا ربطی به بقیه ی اعضا نداره و از هم مستقلند، بنابراین حالتها در هم ضرب میشند و جواب کل برابر با حاصلضرب تعداد حالات حضور همه ی اعضا است. که میشه:
نتیجه گیری:
اگه یه مساله ی یکتا رو با دو روش بشه حل کرد، پس مطمئنا جوابهایی که از راه های متفاوت بدست اومده با هم یکسان و برابر است.
در نتیجه:
موفق باشین.
90/9/9

واقعا ممنونم
خيلي لطف كردين (((:

سوال اول قبلاً در انجمن مطرح شده بود. این رابطه برای همه n های صحیح مثبت برقرار هست. اثبات رو در زیر میتونید ببینید:
برای سوال دوم هم کافیه x=1 , y=1 قرار بدیم حکم ثابت میشه!
هم اکنون 1 کاربر در حال مشاهده این تاپیک میباشد. (0 کاربر عضو شده و 1 مهمان)