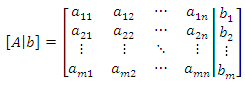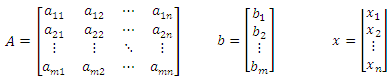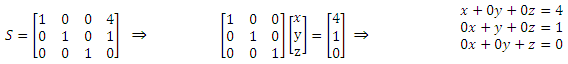بررسی بعضی مباحث ریاضی عمومی 1 و 2 در متلب

**skyzare** · 01-04-2012, 22:34

با سلام .

بررسی دومین تابع :

n = norm ( X ) k این مورد نیز مشابه همان نرم 2 می باشد در واقع اگر نرم یک یا دو را مشخص نکینم به صورت پیش فرض نرم افزار متلب نرم دو را محاسبه می نماید .

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

نرم یک :

در ریاضیات برای نرم یک از فرمول زیر استفاده می شود .

که در واقع به طور ساده ماکزیمم قدر مطلق مجموع هر ستون می باشد .

مثال : نرم یک ماتریس زیر را به دست آورید :

$A=\begin{bmatrix} 1 & 2\\ 3& 4 \end{bmatrix}$

$\\\left \| A \right \|_1=max\left \{ |a_{11}|+|a_{21}|,|a_{12}|+|a_{22}| \right \}= \\\\ max\left \{ 1+3,2+4 \right \}=max\left \{ 4,6 \right \}=6$

بررسی با نرم افزار متلب :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

اگر بخوایم نرم یک را با توجه به فرمول آن و توابع متلب پیاده سازی کنیم به صورت زیر خواهد بود :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

نرم بینهایت :

در ریاضیات برای نرم بی نهایت از فرمول زیر استفاده می شود .

در واقع به طور ساده ماکزیمم قدر مطلق هر سطر ماتریس می باشد .

مثال : نرم بی نهایت ماتریس زیر را به دست آورید .

$A=\begin{bmatrix} 1 & 2\\ 3& 4 \end{bmatrix}$

$\\\left \| A \right \|_1=max\left \{ |a_{11}|+|a_{12}|,|a_{21}|+|a_{22}| \right \}= \\\\ max\left \{ 1+2,3+4 \right \}=max\left \{ 3,7 \right \}=7$

بررسی با نرم افزار متلب :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

اگر بخوایم نرم بی نهایت را با توجه به فرمول آن و توابع متلب پیاده سازی کنیم به صورت زیر خواهد بود :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

توجه شود در تابع sum آرگومان دوم باید عدد 2 گذاشته شود که در واقع به سطر اشاره دارد .

**skyzare** · 01-04-2012, 22:44

Frobenius norm :

برای محاسبه نرم Frobenius از فرمول زیر استفاده می گردد .

که داریم :

در نرم افزار متلب برای محاسبه این نرم از تابع زیر استفاده می شود :

Norm_F = norm ( X , 'fro' )l

مثال : نرم Frobenius ماتریس زیر را به دست آورید .

$A=\begin{bmatrix} 1 &2 \\ 3& 4 \end{bmatrix}$

حل : با توجه به فرمول داریم ( جواب رو با هر دو فرمول می نویسم سومی رو نمیدونم

)

$\left \| A \right \|_F=\sqrt[2]{\sum_{i=1}^{4}\sum_{j=1}^{4}\left | a_{ij} \right |^2}=\sqrt[2]{(1)^2+(2)^2+(3)^2+(4)^2}=5.4774$

اگر با رابطه تریس به دست آوریم :

بررسی با نرم افزار متلب :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

اگر بخوایم نرم فروبینوس را با توجه به فرمول آن و توابع متلب پیاده سازی کنیم به صورت زیر خواهد بود

با توجه به فرمول مجذور سیگما :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

با توجه به تعریف مجذور تریس :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

تابع $norm(v,inf)$ :

در این جا V یک بردار ستونی یا سطری می باشد که با اعمال این تابع به آن بزرگترین درایه V را بر می گرداند .

تابع $norm(v,-inf)$ :

در این جا V یک بردار ستونی یا سطری می باشد که با اعمال این تابع به آن کوچکترین درایه V را بر می گرداند

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

**skyzare** · 02-04-2012, 14:39

با سلام .
اساتید میخواستم یه اطلاعی از عدد حالت ( condition number )به دست بیارم که چیه ؟ البته خودم تا حدودی می دونم . که اگه عدد حالت کوچک باشه یعنی این که ماتریس A و دستگاه حاصل از خوش حالت هست (well ciondition) و اگه بزرگ باشه ماتریس نزدیک به منفرد شدن هست و اون ماتریس بد حالت هست (ill conditiom ). و خطای محاسباتی در معکوس کردن ماتریس A زیاده .

میخواستم بدونم فرمولش چیه ؟ یه چند جا دیدم با هم فرق داشتن .

بعد یه چیز دیگه نوع های مختلفی داره ؟ اخه توی متلب من این جوری دیدم . فرقشون رو نمیدونم چی .

===========================================

این هم تعریفی از دستگاه خوش حالت و بد حالت :

What do you mean by ill-conditioned and well-conditioned system of equations ? l

well-conditioned system : l
A system of equations is considered to be well-conditioned if a small change in the
coefficient matrix or a small change in the right hand side results in a small change in the
solution vector

ill-conditioned : l

A system of equations is considered to be ill-conditioned if a small change in the
coefficient matrix or a small change in the right hand side results in a large change in the
solution vector

===========================================

این لینک هم خوبه :

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

===========================================

**IceLord** · 02-04-2012, 15:43

نوشته شده توسط skyzare [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سوال : فرض کنیم یه چند جمله ای رو توی متلب تعریف کرده باشیم یه چیزی مثل زیر :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

چه جوری میتونم ضرایب چند جمله ای رو از عبارت بالا استخراج کنم ؟؟؟ الان اگه توی اون کد بالا دقت می کردید من برای این که این ضرایب رو به تابع roots بدم خودم دستی وارد کردم .

با سلام

توی متلب می تونید بک چند جمله ای رو به صورت ماتریس هم بیان کنید.

به طور مثال تابع k^2 - 30*k + 4 رو می تونید به صورت [4 30- 1] هم تعریف کنید و در ادامه از دستور

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

استفاده کنید

برای حل اون ماتریس هم می تونید به صورت زیر پیش برید:

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

اگه سوال دیگه ای در زمینه متلب داشتی در حد توان در خدمت هستم.

موفق باشی

**skyzare** · 03-04-2012, 18:50

با سلام .

با تشکر از پاسخ شما :

=======================

با سلام .

منبع :

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

در ابتدا یک بررسی اجمالی بر روی دستگاه ها و شرایط آن خواهیم داشت سپس به بررسی دستورات مربوطه در نرم افزار متلب می پردازیم .

صورت کلی یک دستگاه معادلات جبر خطی با m معادله و n مجهول به شکل زیر در نظر گرفته می شود :

$\\a_{11}x_1+a_{12}x_2+\cdots +a_{1n}x_n=b_1\\\\ a_{21}x_1+a_{22}x_2+\cdots +a_{2n}x_n=b_2\\\\ \: \: \: \: \vdots \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \vdots \: \: \: \: \: \: \: \: \: \:\: \: \: \: \: \: \: \: \: \: \: \: \: \: \vdots \\\\ a_{m1}x_1+a_{m2}x_2+\cdots +a_{mn}x_n=b_m$

این دستگاه معادلات معروف به یک سیستم m*n است که در آن aij و bi مقادیر ثابت و معین و xj مجهولاتی هستند که باید تعیین گردند . این دستگاه معادلات را می توان با صرف نظر کردن مجهولات و فقط با در نظر گرفتن ضرایب به صورت زیر نمایش داد :

این ماتریس را ماتریس افزوده سیستم می نامند ، که هر سطر آن بیان کننده یکی از معادلات خطی می باشد . هم چنین می توان معادلات را به شکل Ax=b نمایش داد که در آن A یک ماتریس m*n ؛ b یک بردار m*1 و x یک بردار n*1 به صورت زیر است :

در رابطه با دستگاه معادلات خطی پرسشی که مطرح می گردد آن است که آیا جوابی برای مجموعه معادلات وجود دارد یا نه . در صورت وجود منحصر به فرد است یا خیر . در فرایند حل این دستگاه معادلات امکان رخ داد حالت های زیر وجود دارد :

1 - حالتی که دستگاه بدون جواب یا ناسازگار است .
2- حالتی که دستگاه سازگار است و جواب دارد که در این صورت امکان دارد فقط یک جواب منحصر به فرد داشته باشد یا این که بی شمار جواب داشته باشد .

**************************************

در یک دستگاه معادلات جبر خطی m*n که m تعداد معادلات و n تعداد مجهولات است حالت های زیر را می توان در نظر گرفت :

حالت m=n : در این حالت دستگاه را همواره معین می گوییم .

اگر $|A|\neq 0$ باشد دستگاه معادلات سازگار است و یک جواب منحصر به فرد دارد

اگر $|A|= 0$ باشد و دستگاه معادلات سازگار باشد بیشمار جواب دارد و برای به دست آوردن یک پاسخ معین از روش حداقل نرم می توان استفاده نمود .

اگر $|A|= 0$ باشد و دستگاه معادلات ناسازگار باشد اصلا جواب ندارد و برای به دست آوردن یک پاسخ تقریبی از روش حداقل مربعات استفاده می شود .

حالت m<n : در این حالت دستگاه را فرومعین گویند .

این گونه سیستم ها می تواند بیشمارش جواب داشته باشد . در دستگاه های فرومعین که دارای بیشمار جواب هستند برای به دست آوردن یک پاسخ معین از روش حداقل نرم می توان استفاده کرد.

حالت m>n : در این صورت دستگاه را فرامعین می نامند .

چنین دستگاه هایی در صورت سازگار بودن می تواند بک جواب منحصر به فرد داشته باشد .
بررسی وجود و یا عدم وجود جواب زمانی که تعداد معادلات و مجهولات دستگاه کم باشند بسیار ساده است . لیکن در عمل ممکن است با تعداد معادلات مجهولات بیشتری سر و کار داشته باشیم . برای دستگاه هایی با تعداد معادلات و مجهولات بیشتر باید از روش های خاصی جهت به دست آوردن پاسخ استفاده کرد. نرم افزار متلب ابزارهای زیادی برای حل دستگاه معادلات خطی دارد . یک روش برای حل دستگاه معادلات Ax=b استفاده از عملگر تقسیم (\) است .

**************************************

در حالت m=n نرم افزار متلب جواب دقیق دستگاه را پس از گرد کردن اعداد محاسبه می نماید .

مثال : دستگاه معادلات زیر را حل نمایید .

$\begin{bmatrix} 1 &2 &3 \\ 4& 5 &6 \\ 7& 8 & 10 \end{bmatrix}\times \begin{bmatrix} x_1\\x_2 \\ x_3 \end{bmatrix}=\begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix}\\\\$

که در آن داریم :

$A=\begin{bmatrix} 1 &2 &3 \\ 4& 5 &6 \\ 7& 8 & 10 \end{bmatrix}$

$X=\begin{bmatrix} x_1\\x_2 \\ x_3 \end{bmatrix}$

$b=\begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix}$

**************************************

حل با متلب استفاده از عملگر ( \ ) : ( اون پایین c=A \ b هست نمیدونم چرا وقتی کد php استفاده می شه چاپ نمیشه !

)

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

============================

حل با روش معکوس کردن A و ضرب در ماتریس b :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

============================

عصر سه شنبه 15 / 1 / 90

**skyzare** · 06-04-2012, 22:46

با سلام .

ادامه حل دستگاه های معادلات جبری خطی :

منبع :

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

در این pdf که به زیان اصلی می باشد بعضی از نکات در نرم افزار متلب و یک سری از توابع از اون رو معرفی کرده که به نظرم جالب هست .

========================================

مقدمه :

استفاده از تابع rref برای حل دستگاه

حل دستگاه های نامنفرد با n معادله و n مجهول :

دستگاه AX=b را در نظر می گیریم که در آن A ماتریس مربعی نامنفرد ( دارای معکوس ) می باشد . که در این حالت دارای یک جواب منحصر به فرد می باشد . یکی از روش های حل آن استفاده از معکوس A می باشد . ولی معمولا این روش پیشنهاد نمی شود زیرا محاسبه معکوس تابع زمان بر می باشد . با استفاده از تابع rref می توان پاسخ را به دست آورد . مزیت این تابع در این می باشد که اگر دستگاه مربعی و منفرد باشد یا مربعی هم نباشد قابل استفاده می باشد در صورتی که دو روش قبلی تنها با دستگاه نامنفرد قابل اعمال است . اساس کار این تابع استفاده از ماتریس افزوده ( Augmented Matrix ) سیستم و محاسبه ماتریس سطری پلکانی ( Reduced row echelon form ) می باشد . ماتریس سطری پلکانی یک ماتریس منحصر به فرد می باشد . که دارای ویژگی های زیر می باشد :
الف ) اولین درایه غیر صفر ( در صورت وجود ) هر سطر ماتریس A برابر با یک ( Called Leading 1 ) می باشد .
ب ) همه درایه های ستونی از A که شامل اولین درایه غیر سطری از A است برابر با صفر باشد .
پ ) اولین درایه غیر صفر هر سطر از اولین درایه غیر صفر سطری بعدی به ستون اول ( دست چپ ) نزدیکتر باشد .
ت ) بعد از سطری که همه درایه های آن صفر است ، سطر غیر صفری وجود نداشته باشد .

================================================== ======

مثال :
دستگاه معادله زیر را حل نمایید . ( با استفاده از به دست آورد ماتریس سطری پلکانی )

$\\0x+2y+0z=2 \\\\ -x+2y-2z=-2\\\\ 0x+y+2z=1$

که ماتریس ضرایب ( A ) و ماتریس مجهول ( X ) و ماتریس طرف دوم ( b ) به صورت زیر است :

$A=\begin{bmatrix} 0 & 2 &0 \\ -1 &2 &-2 \\ 0 &1 &2 \end{bmatrix}$

$X=\begin{bmatrix} x\\y \\z \end{bmatrix}$

$b=\begin{bmatrix} 2\\-2 \\1 \end{bmatrix}$

حل با استفاده از تابع rref :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

در واقع ماتریس S هم ارز با ماتریس افزوده دستگاه اصلی می باشد بنابراین می توان به این صورت عمل کرد :

بنابراین پاسخ به صورت زیر می شود :

x=4 y= 1 z=0

در صورتی که پاسخ را با روش های قبل به دست آوریم خواهیم داشت لازم به ذکر است که به جای استفاده از تابع inv می توان از توان منفی یک نیز استفاده کرد .

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

********************

جمعه 18 فروردین 91

91/1/18

**skyzare** · 08-04-2012, 06:44

با سلام .

ادامه حل دستگاه های معادلات جبری خطی

منبع :

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

=================================================

حالت m<n : تعداد معادله های دستگاه از تعداد مجهولات کمتر است .

برای حل این گونه دستگاه ها نیز می توان از تابع rref استفاده کرد در صورتی که از روش معکوس کردن قادر به حل دستگاه نیستم زیرا ماتریس ضرایب مربعی نبوده در نتیجه قابل معکوس کردن نیست .

مثال :

$\\x_1+3x_2+x_3+5x_4+x_5=5\\\\ 0x_1+x_2+x_3+2x_4+x_5=4\\\\ 0x_1-2x_2-2x_3-3x_4-x_5=-7$

در این مثال تعداد معادلات از تعداد مجهولات کمتر می باشد . ماتریس افزوده دستگاه به فرم زیر می باشد .

$\left.\begin{matrix} 1&3 & 1 & 5 &1 \\ 0&1 &1 &2 &1 \\ 0 & -2 & -2 & -3 & -1 \end{matrix}\right|\begin{matrix}5 \\ 4 \\-7 \end{matrix}$

حال با نرم افزار متلب فرم سطری پلکانی کاهش یافته آن را به دست می آوریم .

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

بنابراین دستگاه اصلی هم ارز با :

$\\x_1-2x_3-x_5=-6\\\\ x_2+x_3-x_5=2\\\\ x_4+x_5=1$

از آنجائیکه تعداد مجهولات بیشتر از تعداد معادلات می باشند ، می توان برخی از مجهولات را بر حسب دیگری به دست آورد . بنابراین دستگاه بی نهایت جواب دارد .

$\\x_1=-6+x_5+2x_3\\\\\\ x_2=2+x_5-x_3\\\\\\ x_4=1-x_5$

و با توجه به این جواب ها ، متغیرهای x1 x2 x4 مستقل نبوده و وابسته به مقدار x5 و x3 هستند

که به x5 و x3 متغیرهای آزاد ( Free Variables ) نیز گفته می شود .

با کمی دقت می توان دریافت که متغیر های x1 x2 x4 مربوط به ستون هایی هستند که عناصر محوری در آنها قرار دارند .

تعریف عناصر محوری : Pivot Entry

اولین درایه غیر صفر ( در صورت وجود ) هر سطر ماتریس سطری پلکانی کاهش یافته برابر با یک می باشد . که به آن عنصر محوری گفته می شود

در شکل زیر نمایی از یک ماتریس سطری پلکانی کاهش یافته مشاهده می شود که یک های با پس زمینه سبز رنگ عناصر محوری می باشند .

==============================================

در حالتی که تعداد معادلات بیشتر از مجهولات باشد نیز به همین صورت عمل می شود .

==============================================

**************************

یکشنبه 20 فروردین 91

91/1/20

**skyzare** · 15-04-2012, 18:07

با سلام .

عنوان : تشخیص سازگار یا ناسازگار بودن دستگاه معادلات با تابع rref

منبع :

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

=================================================

یکی از کاربردهای دستور rref در تشخیص سازگار یا ناسازگار بودن دستگاه معادلات است . معادلات معرفی شده با ماتریس افزوده [A│b] زمانی سازگار است که در فرم سطری پلکانی کاهش یافته یا فرم سطری پلکانی آن ، سطری به شکل زیر ظاهر نشده باشد .

$(0 \: \: 0\: \: 0\: \: ....0\: \: 0\: \: \mid \alpha )$

در غیر این صورت معادله حاصل از سطر مذکور به صورت زیر خواهد آمد :

$0x_1 \: \: + 0x_2\: \:+ 0x_3\: \:+ ....0x_n=\alpha$

که برای $\alpha\neq 0$ این معادله راه حلی ندارد و در نتیجه دستگاه معادلات خطی اصلی ناسازگار خواهد بود .

مثال : سازگاری یا ناسازگاری دستگاه زیر را بررسی نمایید .

$\\2x-y+z=2\\\\ 3x+y-z+t=1\\\\ x+2y-2z-t=4\\\\ x+y-z+t=5$

برای محاسبه دستی باید فرم سطری پلکانی کاهش یافته ماتریس افزوده رو با استفاده از روش حذفی گوس به دست آورد . اگر سطری شرایط ذکر شده در بالا را داشته باشد دستگاه ناسازگار است و هیچ جوابی ندارد .

بررسی با متلب :

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

همان طور که مشاهده می شود اگر بخوایم معادله سطر چهارم ماتریس S را بنویسیم به فرم زیر می شود :

$0x+0y+0z+0t=1$

بنابراین دستگاه اصلا جواب ندارد و ناسازگار می باشد .

البته با استفاده از پیدا کردن رتبه ماتریس افزوده و ماتریس ضرایب و مقایسه این دو می توان سازگاری با ناسازگاری دستگاه را تشخیص داد .

****************************

یکشنبه 27 / 1 / 91

**skyzare** · 15-04-2012, 18:20

با سلام .

عنوان : تشخیص مستقل خطی یا وابسته خطی بودن مجموعه ای از بردار ها با استفاده از تابع rref

منبع :

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

و

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

================================================== ====

تعریف مستقل خطی و وابسته خطی :

بردارهای $u_1\: \: \:,\: \: u_2\: \: \: ,\: \: u_3\: \: \: ,\: \: u_n$ را مستقل خطی ( Linear Independent ) گویند اگر معادله ای به شکل زیر :

$c_1u_1+c_2u_2+c_3_u_3+......+c_nu_n=0$

که در آنها $c_1 \: \: ,\: \: c_2\: \: ,....,c_n$ اسکالرهای ثابتی هستند فقط به ازای شرط

$c_1 = c_2= ....=c_n=0$

برقرار باشد در غیر این صورت برارهای $u_1 \: \: ,\: \: u_2\: \: ,\: \: ...\: \: ,\: \: u_n$ را وابسته خطی ( Linear Dependent ) گویند

نکته : شرط لازم و کافی برای مستقل خطی بودن بردارهای $u_1 \: \: ,\: \: u_2\: \: ,\: \: ...,\: \: u_n$ که هر یک دارای n‌ عنصر هستند آن است که دترمینال ماتریس ضرایب n*n مخالف صفر باشد . زیرا در این صورت دستگاه تنها یک جواب دارد و آن هم بردار صفر می باشد بنابراین شرط مستقل خطی برقرار می شود .

در نرم افزار متلب می توان از دستور $[R \: \: ,\: \: p]=rref(A)$ برای تشخیص استقلال خطی بردارها استفاده نمود. در این جا R فرم سطری پلکانی کاهش یافته و P برداری است که محل عناصر محوری و به عبارتی بردارهای مستقل خطی را نشان می دهد .

================================================== ====

مثال :

استقلال خطی با وابستگی خطی بردارهای زیر را بررسی کنید .

$u_1=\begin{bmatrix} -2\\1 \end{bmatrix}\: \: \: ,\: \: \:u_2=\begin{bmatrix} -1\\-3 \end{bmatrix}\: \: \: ,\: \: \: u_3=\begin{bmatrix} 4\\-2 \end{bmatrix}\: \: \:$

با توجه به تعریف داریم :

$c_1\begin{bmatrix} -2\\1 \end{bmatrix}+c_2\begin{bmatrix} -1\\-3 \end{bmatrix}+ c_3\begin{bmatrix} 4\\-2 \end{bmatrix}=0\: \: \: \: \rightarrow \: \: \: \begin{bmatrix} -2c_1\\ c_1 \end{bmatrix}+\begin{bmatrix} -c_2\\-3c_2 \end{bmatrix}+ \begin{bmatrix} 4c_3\\-2 c_3 \end{bmatrix}=\begin{bmatrix} 0\\0 \end{bmatrix}$

با جمع کردن داریم :

$\begin{bmatrix} -2c_1-c_2+4c_3\\\\ c_1-3c_2-2c_3 \end{bmatrix}=\begin{bmatrix} 0\\\\0 \end{bmatrix}$

دستگاه معادلات و فرم سطری پلکانی کاهش یافته آن به صورت زیر می باشد :

$\begin{bmatrix} -2 & -1 &4 \\ 1& -3 & -2 \end{bmatrix}\begin{bmatrix} c_1\\c_2 \\ c_3 \end{bmatrix}=\begin{bmatrix} 0\\0 \end{bmatrix}\: \: \: \: \rightarrow \: \: \: \: \left [ \left.\begin{matrix} {\color{Red} 1} & 0 &-2 \\ 0& {\color{Red} 1} &0 \end{matrix}\right|\begin{matrix} 0\\0 \end{matrix} \right ]\begin{bmatrix} c_1\\c_2 \\ c_3 \end{bmatrix}$

با توجه به محل عناصر محوری ( یک های قرمز رنگ )‌ متغیر $c_3$ آزاد است و بقیه متغیر ها را می توان بر حسب این متغیر آزاد نوشت :

$c_1=2c_3\: \: \: ,\: \: \: c_2=0$

هم چنین عناصر محوری نشان می دهند که u1 و u2 مستقل خطی و بردار u3 به آنها وابسته است . پس در مجموع بردارهای u1 u2 u3 وابسته خطی می باشند .

================================================== ====

بررسی با متلب :

در نرم افزار متلب می توان از دستور $[R \: \: ,\: \: p]=rref(A)$ برای تشخیص استقلال خطی بردارها استفاده کرد . در این جا R فرم سطری پلکانی کاهش یافته و P برداری است که محل عناصر محوری و به عبارتی بردارهای مستقل خطی را نمایش می دهد .

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

****************************

یکشنبه 27 / 1 / 91

**skyzare** · 15-05-2012, 20:35

با سلام .

این هم یه فایل پیرامون همین موضوع . یه فایل زیپ شده هست که هم فایل ورد و هم فایل pdf و هم فونت های استفاده شده رو داره .

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

نام تاپيک: بررسی بعضی مباحث ریاضی عمومی 1 و 2 در متلب

اختيارات تاپيک

2 کاربر از skyzare بخاطر این مطلب مفید تشکر کرده اند

2 کاربر از skyzare بخاطر این مطلب مفید تشکر کرده اند

این کاربر از skyzare بخاطر این مطلب مفید تشکر کرده است

2 کاربر از IceLord بخاطر این مطلب مفید تشکر کرده اند

این کاربر از skyzare بخاطر این مطلب مفید تشکر کرده است

این کاربر از skyzare بخاطر این مطلب مفید تشکر کرده است

2 کاربر از skyzare بخاطر این مطلب مفید تشکر کرده اند

این کاربر از skyzare بخاطر این مطلب مفید تشکر کرده است

تشخیص مستقل خطی یا وابسته خطی بودن مجموعه ای از بردار ها با استفاده از تابع rref

این کاربر از skyzare بخاطر این مطلب مفید تشکر کرده است

بررسی بعضی از مباحث ریاضی در متلب

2 کاربر از skyzare بخاطر این مطلب مفید تشکر کرده اند

Thread Information

Users Browsing this Thread

User Tag List

قوانين ايجاد تاپيک در انجمن