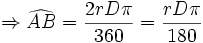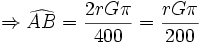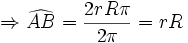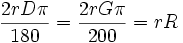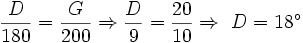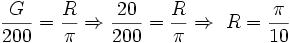توابع مثلثاتی
تعریف روی مثلث قائم الزاویه
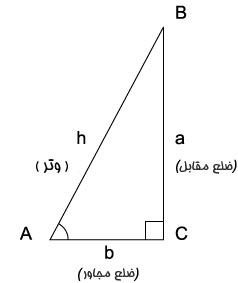
برای تعریف توابع مثلثاتی از یک مثلث قائم الزاویه استفاده می کنیم به عنوان مثال می خواهیم این توابع را برای زاویه A در شکل روبرو تعریف کنیم
ما برای استفاده از این مثلث نامگذاری زیر را انجام می دهیم.
وتر ضلعی است که روبروی زاویه قائم قرار دار که بلندترین ضلع مثلث نیز می باشد و آن را با h نشان داده شده است.
ضلع مقابل زاویه A که آن را با a نشان می دهیم.
ضلع مجاور زاویه قائمه که درشکل با b نشان داده شده است.
حال توابع مثلثاتی را برای زاویه A روی مثلث ABC تعریف می کنیم.
- sin: نسبت ضلع مقابل به وتر را سینوس می گویند یعنی:
- cos: نسبت ضلع مجاور به وتر را گویند یعنی داریم:
- tangent: نسبت ضلع مقابل زاویه به ضلع مجاور را گویند.
- cosecant: نسبت وتر به ضلع مقابل زاویه را گویند.
- secant: نسبت وتر به ضلع مجاور است
- cotangent: نسبت ضلع مجاور به ضلع مقابل را گویند.
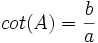




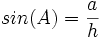
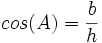
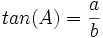
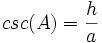
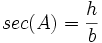

 جواب بصورت نقل قول
جواب بصورت نقل قول استفاده می شود. لذا می توان گفت:
استفاده می شود. لذا می توان گفت: 
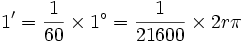
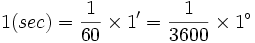
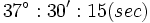



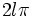 است. یک رادیان اندازه زاویه مرکزی مقابل به کمانی از دایره است که طول کمان روبرو به آن برابر شعاع دایره است.
است. یک رادیان اندازه زاویه مرکزی مقابل به کمانی از دایره است که طول کمان روبرو به آن برابر شعاع دایره است.  رادیان است و زاویه نیم صفحه برابر
رادیان است و زاویه نیم صفحه برابر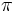 رادیان است. و لذا:
رادیان است. و لذا:  که در آن P محیط دایره است.
که در آن P محیط دایره است.  برابر s و شعاع دایره r باشد آنگاه اندازه زاویه تتا بر حسب رادیان را می توان با یک تناسب ساده چنین محاسبه کرد:
برابر s و شعاع دایره r باشد آنگاه اندازه زاویه تتا بر حسب رادیان را می توان با یک تناسب ساده چنین محاسبه کرد: 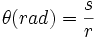
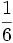 محیط دایره است چند رادیان است؟
محیط دایره است چند رادیان است؟ 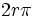 باشد آنگاه اندازه زاویه برابر است با
باشد آنگاه اندازه زاویه برابر است با 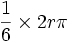 باشد اندازه زاویه چقدر می شود؟
باشد اندازه زاویه چقدر می شود؟ 
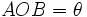 را در دایره در نظر بگیرید:
را در دایره در نظر بگیرید:  =D
=D