بله. از آنجا که اعداد ثابت (جز صفر) چندجمله ای درجه صفر هستند، میتوانرا به صورت ضرب دو چندجمله ای
و 1 نوشت.

بله. از آنجا که اعداد ثابت (جز صفر) چندجمله ای درجه صفر هستند، میتوانرا به صورت ضرب دو چندجمله ای
و 1 نوشت.
با سلام .
اساتید این روابط سری فوریه سینوسی و کسینوسی رو چه جوری از رابطه سری فوریه به دست میارند ؟
خوب این روابط سری فوریه این میشه :

منظور شما از سری فوریه سینوسی و کسینوسی چیست؟
با سلام .
این جوری که حالا توی این جزوه نوشته این جوری گفته که :
محتوای مخفی: تعریف سری فوریه کسینوسی و سینوسی
حالا این که گفته گسترش میدیم یعنی چی ؟ اخه نمیشه که همینجوری به تابع یه چیزی اضافه کنیم . بعد این که این تابع f(x) متناوب هست ؟ اخه توی یه کتاب دیگه گفته بود متناوب ولی این جا این جوری نگفته .
Last edited by skyzare; 17-07-2012 at 12:47.

از آنجا که تابع f تنها در بازهتعریف شده، ما به دنبال سری فوریه ای هستیم که در بازه
، برابر با f باشد، و برایمان مهم نیست که مقدارش در سایر نقاط چیست. بنابراین، در اختیار ما است که مقدار سری فوریه را برای سایر نقاط چگونه تعیین کنیم، یا به زبان دیگر، تابع را چگونه گسترش دهیم. اولین نکته در گسترش تابع اینست که، همانطور که فرمودید، سری فوریه برای یک تابع متناوب تعریف میشود، بنابراین باید تابع را بصورت پریودیک گسترش داد. ساده ترین راه اینست که تابع را با دوره تناوب L، در بازه های متوالی
و از آن طرف
تکرار کنیم. سری فوریه ای که از این روش بدست می آید، معمولاً هم جملات سینوسی را دارد و هم کسینوسی، که ممکن است به فرم مطلوب نباشد.
در حل مسائل مقدار مرزی، گاهی ما به دنبال سری فوریه ای هستیم که تنها جملات سینوسی یا کسینوسی را داشته باشد. برای این مطلوب، ابتدا قرینه تابع نسبت به محور y ها را در بازهاضافه کرده، سپس کل بازه
را با دوره تناوب 2L تکرار می کنیم. در اینصورت، یک تابع پریودیک زوج داریم، و میدانیم که سری فوریه تابع زوج، تنها ضرایب کسینوس را دارد. به طور مشابه، اگر تابع را به طور فرد گسترش میدادیم، تنها ضرایب سینوس را داشتیم.
ترفندهای دیگری نیز قابل اجراست، مثلاً میتوان طوری تابع را گسترش داد که تنها ضرایب فرد را داشته باشد؛ [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ] را ببینید.
Last edited by 1233445566; 17-07-2012 at 13:35.
با سلام .
اساتید من میخوام کانولوشن دو تابع رو به دست بیارم البته خودم محاسبه کردم فقط میخوام بدونم درسته این جوری که رفتم چون یه جور دیکه که میرم جواب صفر میشه .
این دو تابع رو میخوام در هم کانولوشن کنم .
خوب طبق تعریف کانولوشنش این میشه :
من حالا میخوام حاصل این انتگرال بنفش رنگ رو به ازای
به دست بیارم . بنابراین قسمت آبی رنگ در انتگرال بالا که در زیر نوشتم صفر میشه .
پس انتگرال این شکلی میشه :
می تونیم این جوری بگیم که چونهمون بیانگر بازه
پس انتگرال بالا به فرم زیر میشه ؟
با تشکر .
Last edited by skyzare; 19-07-2012 at 23:01.
با سلام .
در واقع مشکلم بیشتر این هست که زیر نوشتم نمی دونم چرا جواب ها یکی نمیشه .
محتوای مخفی: مخفی

نه! در این بازه،و
هر دو برابر 1 هستند، پس عبارت سمت چپ برابر 1، و عبارت سمت راست برابر 0 است. البته وقتی t>0 باشد.
با سلام .
با تشکر از شما .
بله درست می فرمایید . اصلا حواسم نبود . ادم گاهی اوقات توی چه چیزایی گیر می کنه
پس این جوری میشه :
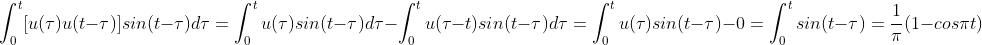
Last edited by skyzare; 20-07-2012 at 18:38.
انتگرال زير را حل كنيد
Last edited by kvhsade; 27-07-2012 at 17:05.
هم اکنون 1 کاربر در حال مشاهده این تاپیک میباشد. (0 کاربر عضو شده و 1 مهمان)