اگر لاپلاس دوطرفه مورد نظر باشد، که به صورت زیر تعریف می شود:
در اینصورت

تبدیل لاپلاس ندارد، چرا که انتگرال فوق به ازای هیچ s ای همگرا نخواهد بود. اما تبدیل لاپلاس

میشود

. حال اگر تابع مورد نظر شما

باشد، میتوانید از قانون تاخیر زمانی استفاده کنید و پاسخ دومتان صحیح است. اما اگر

مورد نظر است، پاسخ اول درست می باشد.
توجه کنید که لاپلاس یکطرفه

برابر است با لاپلاس دوطرفه

. با استفاده از این نکته میتوانید نتایجی را برای لاپلاس یکطرفه استنتاج کنید. همچنین،
سعی کنید قانون تاخیر زمانی را (با یک تغییر متغیر در انتگرال) اثبات نمایید.
با سلام .
با اجازه اساتید من این رو پاسخ بدم . .gif)
اول انتگرال عبارت هایی یه فرم زیر رو در حالت کلی رو به دست میاریم :
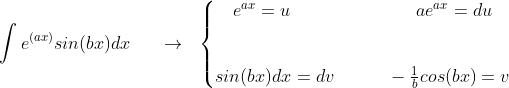
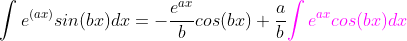
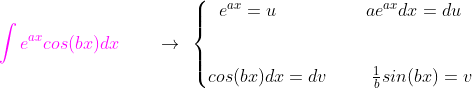
 ====================================
====================================
حالا انتگرال اصلی که در پاین نوشتم رو با اطلاعات بالا به دست میاریم :
فکر کنم با فرض  باند بالا یعنی بی نهایت رو که می زاریم یه عبارت کراندار در صفر ضرب میشه بنابرااین برای کران بالا عبارت صفر میشه . ( درسته ؟ ) بعد از جایگذاری کران پایین به دست می آریم :
باند بالا یعنی بی نهایت رو که می زاریم یه عبارت کراندار در صفر ضرب میشه بنابرااین برای کران بالا عبارت صفر میشه . ( درسته ؟ ) بعد از جایگذاری کران پایین به دست می آریم :
باند بالا یعنی بی نهایت رو که می زاریم یه عبارت کراندار در صفر ضرب میشه بنابرااین برای کران بالا عبارت صفر میشه . ( درسته ؟ ) بعد از جایگذاری کران پایین به دست می آریم :




.gif)

.gif) این جوری درست میشه .
این جوری درست میشه . 




