اتاق ریاضیات(طرح سؤالات)

**Life24** · 21-03-2012, 11:53

سلام
یک مساله ای هست که مثلا 6 نفر دور یک میز هستند و تعداد ترتیب های قرار گرفتنشون میشه

(n-1)!

و مساله حل میشه اما برای درکش مشکل دارم میخوام بدون چرا از تعداد نفرات یکی کم میکنیم ؟
این هم زده به دلیل اینکه ترتیب هایی که دروان دیگری بدست میاد یکسان میگیریم.
یعنی چی/؟

**davy jones** · 23-03-2012, 19:09

نوشته شده توسط iranch [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

دوستان درخت دودویی تقریبا کامل چیه/؟ لطفا دقیق بگوئید که میتونه از سمت چپ هم خالی باشه یا از سمت راست؟
ترتیب پر شدن چطوره/؟

سلام.

سوالتون مربوط به کامپیوتر و رشته ی فناوری اطلاعات میشه و خیلی به ریاضیات مربوط نیست. علی ای حالٍ هر چند که خودم در این زمینه سررشته ای نداشتم ولی یه مقداری سرچ کردم براتون و مقالات زیر یافت شد. تقریبا تو همه ی مقالات سوال شما پاسخ داده شده. البته بایستی تسلط نسبی به زبان انگلیسی داشته باشین. امیدوارم مفید باشه براتون:

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]
[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]
[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

====================

نوشته شده توسط Life24 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سلام
یک مساله ای هست که مثلا 6 نفر دور یک میز هستند و تعداد ترتیب های قرار گرفتنشون میشه

و مساله حل میشه اما برای درکش مشکل دارم میخوام بدون چرا از تعداد نفرات یکی کم میکنیم ؟
این هم زده به دلیل اینکه ترتیب هایی که دروان دیگری بدست میاد یکسان میگیریم.
یعنی چی/؟

سلام.

برای اینکه وقتی یک زنجیره ی حلقوی از افراد تشکیل شد، دیگه فرقی نمیکنه که نفر اول روی کدوم صندلی بشینه. مهم ترتیب و جایگاه افراد نسبت به همدیگه هستش که ترتیب حلقه حفظ بشه. بنابراین اگه اونها رو ساعتگرد یا پاد ساعتگرد دور میز شیفت بدیم، حالت جدیدی ایجاد نمیشه در حالیکه ما این حالات رو در شمارش اولیه لحاظ کردیم. چون به ازای هر چینش دلخواه از این n نفر دور میز، n حالت برای چرخش این چینش خاص زنجیره دور میز و شیفت خوردن اونها در جهت ساعتگرد یا پاد ساعتگرد وجود داره، پس باید تعداد کل حالات جایگشت n نفر بدست اومده رو بر n تقسیم کنیم. دقت کنید که اگه کلمه ی «به ازای هر» صادق نبود، تقسیم کردن صحیح نبود و باید حالت های استثنا رو با عمل تفریق، کم میکردیم نه تقسیم.

موفق باشین.
91/1/4

**Life24** · 23-03-2012, 20:54

میشه این رو برام یک مثال بزنید؟
$C \subset D => C\subseteq D$
وقتی اول زیر مجموعه سره هست بعد چطوری زیر مجموعه میشه؟
یک مورد دیگه هم دارم اول این حل بشه شاید اونم حل شد خودکار

**davy jones** · 23-03-2012, 21:47

نوشته شده توسط Life24 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

میشه این رو برام یک مثال بزنید؟
$C \subset D => C\subseteq D$
وقتی اول زیر مجموعه سره هست بعد چطوری زیر مجموعه میشه؟
یک مورد دیگه هم دارم اول این حل بشه شاید اونم حل شد خودکار

سلام.

تفاوت بین $\subset$ و $\subseteq$ دقیقا مثل تفاوت بین $<$ و $\leq$ هستش. در کوچکتر و کوچکترمساوی، اگر عبارتی کوچکتر از عبارت دیگری باشد، حتما کوچکتر یا مساوی با آن عبارت هم هست. اما عکس این موضوع بدیهیه که درست نیست.

$C \subset D => C\subseteq D$

در اینجا وقتی مجموعه ی C زیرمجموعه ی سره ی D باشه، میتونه زیرمجموعه یا مساوی با D هم باشه. چون ما داریم میگیم یــا. و منظورمون اینه که اگه C زیر مجموعه ی D باشه یا مساوی با خود مجموعه ی D باشه هر دو حالت، مطلوب ماست و کافیه که یکی از این دو شرط برقرار باشه.

موفق باشین.
91/1/4

**Life24** · 24-03-2012, 16:33

اگر ساعت 4 بعد از ظهر روز چهارشنبه باشد. $47^{74}$ چه روزو ساعتتی خواهد بود؟

**davy jones** · 24-03-2012, 20:59

نوشته شده توسط Life24 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

اگر ساعت 4 بعد از ظهر روز چهارشنبه باشد. $47^{74}$ چه روزو ساعتتی خواهد بود؟

سلام. برای اینکه بدونیم $47^{74}$ چه ساعتی میشه، باید باقیمانده ی تقسیم این عدد رو بر 24 بدست بیاریم:

$47^{74}\overset{24}{\equiv }\left (-1 \right )^{74}\overset{24}{\equiv }1$

و این یعنی اگه ساعت 4 بعد از ظهر مبدا زمان باشه، $47^{74}$ ، ساعت 5 بعد از ظهره.

همچنین برای اینکه بدونیم $47^{74}$ چند شنبه میشه، باید باقیمانده ی تقسیم این عدد رو بر 7 بدست بیاریم:

$47^{74}\overset{7}{\equiv }\left (-2 \right )^{74}\overset{7}{\equiv }(-2)^{(3\times 24 +2)}\overset{7}{\equiv }(-8)^{24}+(-2)^{2}\overset{7}{\equiv }(-1)^{24}+4\overset{7}{\equiv }5$

و این یعنی اگه چهارشنبه، مبدا روزهای هفته در نظر گرفته شده باشه، $47^{74}$ ، 5 روز بعد از چهارشنبه یعنی دوشنبه میشه.

پس $47^{74}$ ، نشون دهنده ی ساعت 5 بعد از ظهر روز دوشنبه است.

==================
سوال کاربر محترم، [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ] از بنده در پیغام خصوصی که بعد از اجازه ی ایشون برای استفاده ی سایرین در اینجا قرار میدم:
==================

نوشته شده توسط Life24

شرمنده اقا یک سوال
راستش میخوام خر فهم بشم
$A=\left \{ 1,2,3,4 \right \}$

$U=\left \{ 1,2,3,4,5,6,x,y,\left \{ 1,2 \right \}\left \{ 1,2,3 \right \} \left \{ 1,2,3,4 \right \}\right \}$

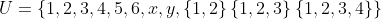
حالا میگیم
$A\subseteq U$
یعنی هر عضو از مجموعه A درون u وجود دارد
$A\subset C$
یعنی عضوی در u است که در A نیست
$A\in U$
یعنی مجموعه a به عنوان یک عنصر درون u وجود دارد منظور اینه
$A=\left \{ 1,2,3,4 \right \}$

تا اینجا درست؟

اما این ها گیچ میشم

$\left \{ A \right \} \subseteq U$
$\left \{ A \right \} \subset U$
$\left \{ A \right \}\notin U$

مخوصا مورد اخر توجیهی براش ندارم

سلام.
دشمنتون شرمنده.

چه خوب بود که این سوال رو هم تو همون تاپیک اتاق ریاضیات میپرسیدین تا اگه سایر عزیزان و کاربران فعال اونجا هم نظری دارند ارائه بدند و هم اینکه این سوال به نوعی اونجا آرشیو بشه تا اگه سوال کاربران دیگه ای هم بعدا همین بود، با یه سرچ میتونستند جواب بگیرن. به هر حال ...

الان تو این مجموعه ی A و U ای که شما نوشتین داریم: $A\subset U$ چون: $A=\left \{ 1,2,3,4 \right \}$ و در U عضوهای 1 و 2 و 3 و 4 وجود داره (منظورم اعضاییه که قرمز رنگشون کردم):

$U=\left \{ {\color{Red} \mathbf{1,2,3,4}},5,6,x,y,\left \{ 1,2 \right \},\left \{ 1,2,3 \right \},\left \{ 1,2,3,4 \right \} \right \}$

خب همونطور که قبلا هم بحث شد، اگر به ازای هر A و U دلخواه داشته باشیم $A\subset U$ پس حتما رابطه ی $A\subseteq U$ هم درسته و استدلال جدیدی نداره.

$A\subseteq U$
یعنی هر عضو از مجموعه A درون u وجود دارد
$A\subset C$
یعنی عضوی در u است که در A نیست

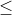
این استدلال خیلی درست نیست. چرا که در هر دو حالت ممکنه که عضوی از U وجود داشته باشه که در A نباشه و همچنین در هر دو حالت حتما هر عضو A درون U وجود داره. باز هم تاکید میکنم که مفهوم کوچکتر (>) و کوچکتر مساوی ( $\leq$ ) رو تو ذهنتون یادآوری کنین.

------
و اما داریم: $A\in U$ چون همونطور که خودتون هم اشاره کردین مجموعه ی A به عنوان یک عضو یا عنصر، در U موجوده:

$U=\left \{ 1,2,3,4,5,6,x,y,\left \{ 1,2 \right \},\left \{ 1,2,3 \right \},{\color{Red} \left \{ 1,2,3,4 \right \}} \right \}$

-----

وقتی میخوایم عضو یا اعضایی از یک مجموعه رو نشون بدیم، اونها رو به تنهایی نشون میدیم و دور اون عضو یا اعضا، آکولاد { } نمیذاریم. مثلا در همون U میگیم: $x\in U$
اما وقتی که بخوایم زیر مجموعه های یک مجموعه رو نشون بدیم، باید حتما اون زیر مجموعه، خودش یک مجموعه باشه و باید دورش آکولاد بذاریم. یعنی باید اینطوری بنویسیم: $\left \{ x \right \} \subset U$ یا $\left \{ x \right \}\subseteq U$

بنابراین وقتی که میگیم: $A\subset C$ منظورمون اعضای قرمز رنگ زیره:

$U=\left \{ {\color{Red} \mathbf{1,2,3,4}},5,6,x,y,\left \{ 1,2 \right \},\left \{ 1,2,3 \right \},\left \{ 1,2,3,4 \right \} \right \}$

اما وقتی که میگیم: $\left \{ A \right \} \subset U$ منظورمون از $\left \{ A \right \}$ مجموعه ایه که A عضوش باشه یعنی اینطوری: $\left \{ \left \{ 1,2,3,4 \right \} \right \}$
پس منظورمون از $\left \{ A \right \} \subset U$ عضو قرمز رنگ زیر هستش:

$U=\left \{ 1,2,3,4,5,6,x,y,\left \{ 1,2 \right \},\left \{ 1,2,3 \right \},{\color{Red} \left \{ 1,2,3,4 \right \}} \right \}$

به همین حالت و دقیقا با همین استدلال، $\left \{ A \right \} \subseteq U$ هم نشون داده میشه که درست و صادق هستش.

-----

اما در $\left \{ A \right \}\notin U$ ، با توجه به توضیحاتی که داده شد (برای نشون دادن اعضا، آکولاد به کار نمیره و فقط برای نشون دادن زیرمجموعه ها از آکولاد استفاده میکنیم) در اینجا $\left \{ A \right \}$ در حقیقت برابر با $\left \{ \left \{ 1,2,3,4 \right \} \right \}$ هستش و چون U عضوی به صورت $\left \{ \left \{ 1,2,3,4 \right \} \right \}$ نداره، پس $\left \{ A \right \}$ عضو U نیست و داریم: $\left \{ A \right \}\notin U$

==========

حالا برای اینکه متوجه بشم که متوجه توضیحات من شدید، یه سوال نسبتا سخت هم بنده در این زمینه طرح میکنم:

مجموعه ی M رو به صورت زیر در نظر بگیرین:

$M=\left \{ \varnothing ,\left \{ \varnothing \right \} ,\left \{ \varnothing ,\varnothing \right \},\left \{ \left \{ \varnothing \right \} \right \},\left \{ \varnothing ,\left \{ \varnothing \right \} \right \}\right \}$

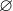
منظور از $\varnothing$ همون مجموعه ی تهی هستش.

الف) مجموعه ی M چند عضو دارد؟
ب) درستی عبارات زیر را بررسی کنید:

1- $\varnothing \subseteq M$
2- $\left \{ \varnothing \right \}\subseteq M$
3- $\left \{ \left \{ \varnothing \right \} \right \}\subseteq M$
4- $\left \{ \left \{ \left \{ \varnothing \right \} \right \} \right \}\subseteq M$
5- $\left \{ \left \{ \left \{ \left \{ \varnothing \right \} \right \} \right \} \right \}\subseteq M$
6- $\varnothing ,\left \{ \varnothing \right \}\in M$
7- $\left \{ \varnothing ,\left \{ \varnothing \right \} \right \}\in M$
8- $\left \{ \varnothing ,\left \{ \varnothing \right \} \right \}\subseteq M$
9- $\left \{ \left \{ \varnothing ,\left \{ \varnothing \right \} \right \} \right \}\subseteq M$
10- $\left \{ \varnothing ,\left \{ \varnothing \right \},\left \{ \left \{ \varnothing \right \} \right \} \right \}\subseteq M$

اگه تمایل دارین پاسخ ها رو با نقل قول گرفتن از صورت سوال در اتاق ریاضیات بگذارین تا اونجا سایر دوستان هم بیان و نظرشون رو بگن. همچنین اگه اجازه بدین توضیحات این پیغام خصوصی رو هم تو اتاق ریاضیات قرار بدم.
==================

نوشته شده توسط Life24

سلام بر شما
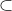
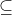
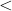
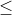
من نمیفهمم تفاوت بین $\subset$ و $\subseteq$ دقیقا مثل تفاوت بین $<$ و $\leq$ هستش. در کوچکتر و کوچکترمساوی، اگر عبارتی کوچکتر از عبارت دیگری باشد، حتما کوچکتر یا مساوی با آن عبارت هم هست.

چطور ممکنه؟ میشه مثالی بزنید من این رو بد متوجه شدم و یک چیز دیگه ظاهرا رفته تو مغزم

A={1,2,3}0
B={1,2}0
الان b زیر مجموعه سره هست چطور مساوی این میشه طبق گفته شما>؟

سلام.

ببینین این تعاریف خیلی چیز شاقی نیستن که خودتون رو باهاش اذیت کنین.

ما میدونیم و مطمئنیم که 10>2
مثلا وقتی مینویسیم $2\leq 10$ ، به نظرتون آیا این نامساوی برقرار و صحیح هست یا نه؟
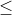
معلومه که برقراره و درسته. چون 2 کوچکتر یا مساوی با 10 هستش. وقتی از علامت $\leq$ استفاده میکنیم لزوما دوطرف نامساوی نباید با هم برابر باشن که. میتونن برابر هم باشند و میتونه طرف سمت چپ کوچکتر از سمت راست هم باشه.

حالا وقتی مینویسیم $A\subseteq B$ یعنی A یا برابر با خود B هستش و یا زیرمجموعه ی سره ی B. و اگر از قبل میدونستیم که A زیر مجموعه ی سره ی B هست (یعنی: $A\subset B$ ) بنابراین با خیال راحت میتونیم صحت و درستی عبارت $A\subseteq B$ رو هم اثبات کنیم. چون در این حالت شرط عوض نشده و فقط یک شرط جدید به مساله اضافه شده که میگه یا این یا اون هر کدومشون که درست باشه، شرط برقرار و درسته.

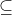
تو منطق، عملگر های And و Or رو دیدی تا حالا؟ اگه دیدین، $\subseteq$ مثل Or میمونه.

A={1,2,3}0
B={1,2}0
الان b زیر مجموعه سره هست چطور مساوی این میشه طبق گفته شما>؟

قرار نیست که مساوی باشن حتما که ...
قراره یا مساوی باشند یا B زیرمجموعه ی A باشه که هست.

موفق باشین.
91/1/5

**skyzare** · 24-03-2012, 22:48

مجموعه ی M رو به صورت زیر در نظر بگیرین:

$M=\left \{ \varnothing ,\left \{ \varnothing \right \} ,\left \{ \varnothing ,\varnothing \right \},\left \{ \left \{ \varnothing \right \} \right \},\left \{ \varnothing ,\left \{ \varnothing \right \} \right \}\right \}$

منظور از $\varnothing$ همون مجموعه ی تهی هستش.

الف) مجموعه ی M چند عضو دارد؟
ب) درستی عبارات زیر را بررسی کنید:

1- $\varnothing \subseteq M$
2- $\left \{ \varnothing \right \}\subseteq M$
3- $\left \{ \left \{ \varnothing \right \} \right \}\subseteq M$
4- $\left \{ \left \{ \left \{ \varnothing \right \} \right \} \right \}\subseteq M$
5- $\left \{ \left \{ \left \{ \left \{ \varnothing \right \} \right \} \right \} \right \}\subseteq M$
6- $\varnothing ,\left \{ \varnothing \right \}\in M$
7- $\left \{ \varnothing ,\left \{ \varnothing \right \} \right \}\in M$
8- $\left \{ \varnothing ,\left \{ \varnothing \right \} \right \}\subseteq M$
9- $\left \{ \left \{ \varnothing ,\left \{ \varnothing \right \} \right \} \right \}\subseteq M$
10- $\left \{ \varnothing ,\left \{ \varnothing \right \},\left \{ \left \{ \varnothing \right \} \right \} \right \}\subseteq M$

اگه تمایل دارین پاسخ ها رو با نقل قول گرفتن از صورت سوال در اتاق ریاضیات بگذارین تا اونجا سایر دوستان هم بیان و نظرشون رو بگن. همچنین اگه اجازه بدین توضیحات این پیغام خصوصی رو هم تو اتاق ریاضیات قرار بدم.

با سلام .

بفرمایید این نظر من . مطمئن نیستم درست میگم با نه .(

‌)

الف : فکر کنم مجموعه M دارای 4 عضو باشه . به نظر میاد این ها یکی باشه .

$\left \{ \phi \right \}=\left \{ \phi \: ,\: \phi \right \}$

ب :

1- درست

2- درست

3-درست

4-درست

5-غلط

6-درست

7-درست

8-درست

9-درست

10-درست

===================================

اگه همه اش اشتباه بود ..........بهم نخندیدن ها ...

================================================== =====

میشه یه توضیحی هم درباره این بدید .

$47^{74}\overset{24}{\equiv }\left (-1 \right )^{74}\overset{24}{\equiv }1$

**Life24** · 24-03-2012, 23:38

مجموعه ی M رو به صورت زیر در نظر بگیرین:

$M=\left \{ \varnothing ,\left \{ \varnothing \right \} ,\left \{ \varnothing ,\varnothing \right \},\left \{ \left \{ \varnothing \right \} \right \},\left \{ \varnothing ,\left \{ \varnothing \right \} \right \}\right \}$

منظور از $\varnothing$ همون مجموعه ی تهی هستش.

الف) مجموعه ی M چند عضو دارد؟
ب) درستی عبارات زیر را بررسی کنید:

1- $\varnothing \subseteq M$
2- $\left \{ \varnothing \right \}\subseteq M$
3- $\left \{ \left \{ \varnothing \right \} \right \}\subseteq M$
4- $\left \{ \left \{ \left \{ \varnothing \right \} \right \} \right \}\subseteq M$
5- $\left \{ \left \{ \left \{ \left \{ \varnothing \right \} \right \} \right \} \right \}\subseteq M$
6- $\varnothing ,\left \{ \varnothing \right \}\in M$
7- $\left \{ \varnothing ,\left \{ \varnothing \right \} \right \}\in M$
8- $\left \{ \varnothing ,\left \{ \varnothing \right \} \right \}\subseteq M$
9- $\left \{ \left \{ \varnothing ,\left \{ \varnothing \right \} \right \} \right \}\subseteq M$
10- $\left \{ \varnothing ,\left \{ \varnothing \right \},\left \{ \left \{ \varnothing \right \} \right \} \right \}\subseteq M$

5 عضو دارد

ب)
1.غلط
2.درست
3.درست
4.درست
5.اشتباه
6.درست
7.درست
8.درست
9.درست
10.درست

خواستم تو عید خنده تون رو جور کرده باشم

**hts1369** · 25-03-2012, 09:06

سلام
سال نو مبارک
یه سوال در مورد به توان رسوندن یک ماتریس
وقتی یه ماتریس رو میخواهیم به توان سه برسونیم
باید کدوم یکی از کارها رو بکنیم
$A^3=A^{2}A$ یا $A^3=AA^{2}$ البته من هرماتریسی رو امتحان میکنم یه جوابی که بدست میاد یه چیز میشه .
در حالت کلی با هم برابر هستن؟

**davy jones** · 25-03-2012, 11:25

نوشته شده توسط skyzare [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

با سلام .

بفرمایید این نظر من . مطمئن نیستم درست میگم با نه .(

‌)

الف : فکر کنم مجموعه M دارای 4 عضو باشه . به نظر میاد این ها یکی باشه .

$\left \{ \phi \right \}=\left \{ \phi \: ,\: \phi \right \}$

ب :

1- درست

2- درست

3-درست

4-درست

5-غلط

6-درست

7-درست

8-درست

9-درست

10-درست

===================================

اگه همه اش اشتباه بود ..........بهم نخندیدن ها ...

================================================== =====

میشه یه توضیحی هم درباره این بدید .

$47^{74}\overset{24}{\equiv }\left (-1 \right )^{74}\overset{24}{\equiv }1$

سلام. جواب هاتون همگی درست اند. اگه دوست داشتین در مورد چرایی جوابهای خودتون در هر قسمت هم یه توضیحی بدید.

میشه یه توضیحی هم درباره این بدید .

$47^{74}\overset{24}{\equiv }\left (-1 \right )^{74}\overset{24}{\equiv }1$

در هم نهشتی، هر مضرب دلخواه از پیمانه ی هم نهشتی (که به هر توان دلخواهی هم رسیده باشه) تاثیری در جواب نهایی نمیذاره. به عبارت دیگه و به بیان ساده تر اگه عددی که میخواهیم باقیمانده ی تقسیم اون عدد رو به 24 حساب کنیم، عامل 24 داشته باشه، میتونیم اون عامل رو تا اونجایی که میتونیم ساده و حذف کنیم و این کار تاثیری در مقدار باقیمانده ی نهایی تقسیم نمیذاره. همچنین اگه بتونیم اون عدد رو به صورت مجموع 2 یا چند عدد که برخی از اونها عامل 24 (منظور عامل عدد پیمانه) رو دارند در بیاریم، چون باقیمانده ی تقسیم قسمتهایی که مضرب 24 هستند، بر 24 برابر با صفر میشه، میتونیم اونها رو حذف کنیم و به همین ترتیب، عدد اولیه رو ساده تر کنیم:

$47^{74}\overset{24}{\equiv }(2\times 24-1)^{74}\overset{24}{\equiv }\sum_{k=0}^{74} \binom{74}{k}(2\times 24)^{k}(-1)^{74-k}\overset{24}{\equiv }(-1)^{74}\overset{24}{\equiv }1$

در اینجا در بسط دو جمله ای، همه ی جملات، به جز جمله ی $(-1)^{74}$ ، عامل 24 دارند و بنابراین باقیمانده ی تقسیم اونمها بر 24 صفر میشه و تاثیری در جواب کل نمیذارن.

یکی از متداول ترین روشهای حل چنین مسائلی، پیدا کردن ضریبی از عدد پیمانده است که با مقدار پایه ی توان عدد موجود در سمت چپ، یک واحد اختلاف داشته باشد. در اینصورت، مقدار توان عدد سمت چپ، هر چه که باشد مهم نیست چرا که در حقیقت به $1^{n}$ یا $(-1)^{n}$ میرسیم.

اگه بازم توضیح نیاز داره بگین تا در خدمتتون باشم. اما فکر کنم، این مباحث رو شما در درس ریاضیات گسسته ی پیشدانشگاهی شاخه ی ریاضی فیزیک، قبلا گذروندین.

===============

نوشته شده توسط Life24 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

5 عضو دارد

ب)
1.غلط
2.درست
3.درست
4.درست
5.اشتباه
6.درست
7.درست
8.درست
9.درست
10.درست

خواستم تو عید خنده تون رو جور کرده باشم

سلام.

به جوابهای کاربر گرامی، جناب [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ] مراجعه کنین.

===================

نوشته شده توسط hts1369 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سلام
سال نو مبارک
یه سوال در مورد به توان رسوندن یک ماتریس
وقتی یه ماتریس رو میخواهیم به توان سه برسونیم
باید کدوم یکی از کارها رو بکنیم
$A^3=A^{2}A$ یا $A^3=AA^{2}$ البته من هرماتریسی رو امتحان میکنم یه جوابی که بدست میاد یه چیز میشه .
در حالت کلی با هم برابر هستن؟

سلام.
در اینجا فرقی نمیکنه:

$A^{3}=A\times A^{2}=A\times (A\times A)=(A\times A)\times A=A^{2}\times A$

البته فکر کنم تعریف دوم شما، اصولی تر باشه چون همیشه ماتریس جدید، از سمت چپ ضرب شدنش در نظر گرفته میشه

موفق باشین.
91/1/6

نام تاپيک: اتاق ریاضیات(طرح سؤالات)

اختيارات تاپيک

این کاربر از Life24 بخاطر این مطلب مفید تشکر کرده است

2 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

این کاربر از Life24 بخاطر این مطلب مفید تشکر کرده است

2 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

این کاربر از Life24 بخاطر این مطلب مفید تشکر کرده است

5 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

2 کاربر از skyzare بخاطر این مطلب مفید تشکر کرده اند

2 کاربر از Life24 بخاطر این مطلب مفید تشکر کرده اند

این کاربر از hts1369 بخاطر این مطلب مفید تشکر کرده است

3 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

Thread Information

Users Browsing this Thread

User Tag List

قوانين ايجاد تاپيک در انجمن