اتاق ریاضیات(طرح سؤالات)

**skyzare** · 10-03-2012, 22:32

با سلام .

اساتید ببخشید بردار های ویژه این عبارت رو چه جوری میشه ؟

این هم دستگاه هش که بعد از به دست اوردن مقدار ویژها این جوری شده . میدونم باید لاندا رو جایگزین کنم ولی بعدش رو دقیقا نمیدونم چه جوری به دست میاره .

$\\\lambda _1=\lambda _2=1 \: \: \: \:\lambda _3=3 \\ \\(2 -\lambda )x+y=0\\\\ x+( 2-\lambda )y=0\\\\ ( 1-\lambda )z=0$

با تشکر .

**davy jones** · 12-03-2012, 20:10

نوشته شده توسط skyzare [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

با سلام .

اساتید ببخشید بردار های ویژه این عبارت رو چه جوری میشه ؟

این هم دستگاه هش که بعد از به دست اوردن مقدار ویژها این جوری شده . میدونم باید لاندا رو جایگزین کنم ولی بعدش رو دقیقا نمیدونم چه جوری به دست میاره .

$\\\lambda _1=\lambda _2=1 \: \: \: \:\lambda _3=3 \\ \\(2 -\lambda )x+y=0\\\\ x+( 2-\lambda )y=0\\\\ ( 1-\lambda )z=0$

با تشکر .

سلام.

اصل ماتریس اولیه چی بوده؟

موفق باشین.
90/12/22

**skyzare** · 13-03-2012, 11:39

نوشته شده توسط davy jones [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سلام.

اصل ماتریس اولیه چی بوده؟

موفق باشین.
90/12/22

با سلام .

با تشکر از شما .

ماتریس اصلی این بوده :

$A=\begin{bmatrix} 2 &1 &0 \\ 1& 2 &0 \\ 0& 0 &1 \end{bmatrix}$

**davy jones** · 13-03-2012, 19:52

نوشته شده توسط skyzare [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

با سلام .

با تشکر از شما .

ماتریس اصلی این بوده :

$A=\begin{bmatrix} 2 &1 &0 \\ 1& 2 &0 \\ 0& 0 &1 \end{bmatrix}$

سلام.

طبق تعریف هر ماتریس دلخواه مانند:

$w=\begin{bmatrix} x\\ y\\ z \end{bmatrix}$

که در اون z=0 باشه مطمئنا میتونه بردار ویژه ی ماتریس A باشه. اگه لاندا رو برابر با 1 فرض بشه، z میتونه مخالف 0 هم باشه و هر عدد دلخواه باشه.

وقتی در معادله ی همگن $(A-\lambda I)w=0$ خودمون میایم و مقدار دترمینان $A-\lambda I$ رو برابر با صفر میذاریم به این جهته که معادله ی همگن فوق جوابی به جز صفر هم داشته باشه. در اون صورت هر بردار دلخواهی مانند w بردار ویژه ی ماتریس A خواهد بود. دقیقا مشابه معادله ی خطی ax=0 که اگه خودمون ضریب a رو برابر با صفر قرار بدیم، متغیر معادله (یعنی x) میتونه مقادیر ناصفر رو هم اتخاذ کنه و هر مقدار دلخواه متناهی باشه.

برای مطالعه ی بیشتر به لینک زیر مراجعه کنین:
[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

موفق باشین.
90/12/23

**Life24** · 14-03-2012, 18:11

$\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}1$

لطفا ثابت کنید این چطوری به
$\frac{n}{2}(n-1)$

رسید؟ یک فرمولی داره اگر اشتباه نکنم انتها - ابتدا و از این چیزها ممنون

**davy jones** · 14-03-2012, 19:17

نوشته شده توسط Life24 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

$\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}1$

لطفا ثابت کنید این چطوری به
$\frac{n}{2}(n-1)$

رسید؟ یک فرمولی داره اگر اشتباه نکنم انتها - ابتدا و از این چیزها ممنون

سلام.

در سری ها اگر c یک عدد ثابت فرض شود (و نه یک متغیر) داریم:

$\sum_{j=a}^{b}c=(b-a+1)\times c$

پس در مورد $\sum_{j=i+1}^{n-1}1$ میتوان گفت:

$\sum_{j=i+1}^{n-1}1=n-i-1$

پس داریم:

$\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}1=\sum_{i=0}^{n-2}(n-i-1)=\sum_{i=0}^{n-2}n-\sum_{i=0}^{n-2}i-\sum_{i=0}^{n-2}1=n(n-1)-\frac{(n-2)(n-1)}{2}-(n-1)=(n-1)(n-\frac{n}{2}+1-1)=(n-1)\times \frac{n}{2}={\color{Golden} \frac{n(n-1)}{2}}$

موفق باشین.
90/12/24

**Life24** · 14-03-2012, 22:02

خیلی ممنون از توضیحات شما
راستی میشه این رو هم بگید . میدانم چطوری حساب میشه اما میخوام راه اثباتش بدونم. همین میگن انتها + ابتدا و از این چیزها
کلا از کدام منبع یا سایتی میشه این سری ها رو با اثبات و فرول های کلی یاد گرفت . واقعا لازمشون دارم
$\sum_{i=1}^{n}i$

**davy jones** · 14-03-2012, 23:05

نوشته شده توسط Life24 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

خیلی ممنون از توضیحات شما
راستی میشه این رو هم بگید . میدانم چطوری حساب میشه اما میخوام راه اثباتش بدونم. همین میگن انتها + ابتدا و از این چیزها
کلا از کدام منبع یا سایتی میشه این سری ها رو با اثبات و فرول های کلی یاد گرفت . واقعا لازمشون دارم
$\sum_{i=1}^{n}i$

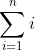
سلام.

موقعی که عبارت داخل سری از جنس متغیر حدود بالا و پایین سری (به عبارت دیگه متغیر شمارنده یا شماره انداز سری) نیست، در محاسبه حکم یه عدد ثابت رو داره. در محاسبه ی این سریها مثل این میمونه که شما به تعدادی که حدود بالا و پایین سری مشخص کرده، دارین یه مقدار ثابت رو مدام با خودش جمع میکنین. حالا سوال اینه که حدود سری رو چطوری میشه فهمید که چند تاست؟ مثلا در عبارت زیر:

$\sum_{i=a}^{b}x$

متغیر سری برابر با i هستش، نه x. بنابراین در اینجا x مثل یه عدد ثابت میمونه و حاصل سری برابر میشه با مجموع تعدادی x. اما چند تا؟ در واقع باید پرسید که از a تا b چند تا عدد صحیح وجود داره؟ جواب اینه که بین هر دو عدد صحیح دلخواه a و b، با احتساب خود a و b، تعداد b-a+1 عدد صحیح وجود داره.

البته من هیچوقت افراد رو به حفظ کردن چنین قاعده های گفتاری تشویق و ترغیب نمیکنم. همین که شما یکبار راه اصولیش رو ببینین بای همیشه تو ذهنتون خواهد موند. اما اگه واقعا اصرار دارین و فکر میکنین که اونطوری راحت تر تو ذهن شما میمونه، قاعده اش اینه: کران بالا رو منهای کران پایین به علاوه ی یک

البته همونطور که گفتم این فقط مختص زمانیه که عبارت داخل سری از جنس متغیر موجود در کران سری نباشه.

و اما در مورد سریهایی به فرم $\sum_{i=1}^{n}i$ که در واقع مجموع اعداد طبیعی متوالی از 1 تا هر عدد دلخواه هستند. بد نیست که یکبار هم راه اثبات فرمولش رو بدونین:

اگه این سری رو باز کنیم خواهیم داشت:

$\sum_{i=1}^{n}i=1+2+3+...+(n-1)+n$

اما میشه جملات رو دو تا دو تا به صورت یکی از ابتدا و یکی از انتها نوشت:

${\color{Red} 1}+{\color{Green} 2}+{\color{Blue} 3}+...{\color{Blue} (n-2)}+{\color{Green} (n-1)}+{\color{Red} n}={\color{Red} (n+1)}+{\color{Green} (n-1+2)}+{\color{Blue} (n-2+3)}+...=(n+1)+(n+1)+(n+1)+...$

میبینیم که حاصل هر پرانتز برابر با n+1 میشه. حالا باید فهمید که چند تا پرانتز داریم؟ چون تعداد کل اعداد موجود n تا بود و ما اونها رو در دسته های 2 تایی قرار دادیم، پس تعداد پرانتزها برابر با $\frac{n}{2}$ هستش. پس مجموع $\frac{n}{2}$ تا عبارت n+1 میشه: $\frac{n}{2}(n+1)$

پس:

$\sum_{i=1}^{n}i=\frac{n(n+1)}{2}$

اما ممکنه که سوال پیش بیاد که اگه تعداد n زوج نبود چی؟ چون ما فرض کردیم که میشه تعداد n عدد رو به دسته های 2 تایی تقسیم کرد. اگه n فرد هم باشه طبق همین روش و قاعده $\frac{n-1}{2}$ تا دسته ی دو تایی تشکیل میشه که حاصل هر کدوم از اون دسته ها برابر با n+1 میشه و مقدار اون عدد وسط در این سری هم خودش برابر با میانگین حسابی کران بالا و پایین سری هستش. پس حاصل سری در این حالت برابر میشه با:

$\frac{n-1}{2}(n+1)+\frac{n+1}{2}=\frac{(n^{2}-1)+(n+1)}{2}=\frac{n^{2}+n}{2}=\frac{n(n+1)}2{}$

که برابر با همون مقدار قبلی هستش در موقعی که n زوج فرض شده بود. بنابراین در حالت کلی ثابت میشه.

--

برای مطالعه ی بیشتر در مورد سریها به منابع زیر میتونین مراجعه کنین:

منابع لاتین:

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]
[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

منابع فارسی:

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]
[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

موفق باشین.
90/12/24

***M!L4D*** · 15-03-2012, 23:48

اساتید این سوال رو درست حل کردم ؟!

**iranch** · 19-03-2012, 20:15

دوستان درخت دودویی تقریبا کامل چیه/؟ لطفا دقیق بگوئید که میتونه از سمت چپ هم خالی باشه یا از سمت راست؟
ترتیب پر شدن چطوره/؟

نام تاپيک: اتاق ریاضیات(طرح سؤالات)

اختيارات تاپيک

بردار ویژه

این کاربر از davy jones بخاطر این مطلب مفید تشکر کرده است

2 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

این کاربر از Life24 بخاطر این مطلب مفید تشکر کرده است

3 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

این کاربر از Life24 بخاطر این مطلب مفید تشکر کرده است

2 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

4 کاربر از M!L4D بخاطر این مطلب مفید تشکر کرده اند

Thread Information

Users Browsing this Thread

User Tag List

قوانين ايجاد تاپيک در انجمن

نام تاپيک: اتاق ریاضیات(طرح سؤالات)

اختيارات تاپيک

بردار ویژه

این کاربر از davy jones بخاطر این مطلب مفید تشکر کرده است

2 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

این کاربر از Life24 بخاطر این مطلب مفید تشکر کرده است

3 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

این کاربر از Life24 بخاطر این مطلب مفید تشکر کرده است

2 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

4 کاربر از *M!L4D* بخاطر این مطلب مفید تشکر کرده اند

Thread Information

Users Browsing this Thread

User Tag List

قوانين ايجاد تاپيک در انجمن

4 کاربر از M!L4D بخاطر این مطلب مفید تشکر کرده اند