داش حمید دنبال غلط املایی نباش که کلا غلطم
در مورد مشتق فک کنم یه اشتباهی کرده باشین
چون مشتق بدست اومده هیچ وقت برابر با صفر نمیشه پس این تابع نقطه بحرانی نداره.
کاربر عزیز Greedy
اين دستگاه رو ميشه به هر روشي حل کرد ولي يکي از راحتترين روشها اينه که تو يکي از معادلات يکي از مجهولات رو بر حسب دوتاي ديگه بدست بياري و تو دوتا معادله ي بعدي قرار بدي(البته من براي حل معادله ي شما از اين روش استفاده نکردم!)
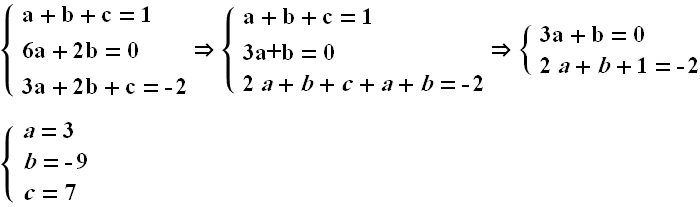




.gif) ولی الآن طبق عرایض قبلی بنده، خودتون بررسی کنین که کدوم زوج مرتب هایی از x و y هایی که بدست آوردین باعث میشن که هم
ولی الآن طبق عرایض قبلی بنده، خودتون بررسی کنین که کدوم زوج مرتب هایی از x و y هایی که بدست آوردین باعث میشن که هم .gif)
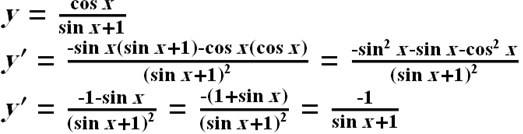


.gif) خداییش دیگه دستم از تایپ کردن خسته شد)
خداییش دیگه دستم از تایپ کردن خسته شد)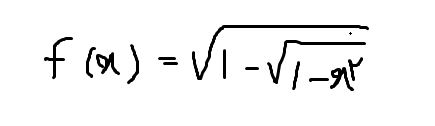 هم خدایی خیلی فرق داره بالا
هم خدایی خیلی فرق داره بالا .gif)
.gif)

.gif)

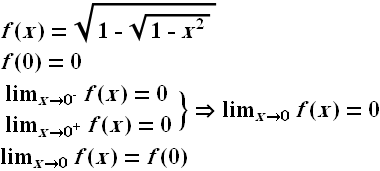
.gif)
.gif) )
)
