در اینجا من در حقیقت اومدم و جملات مثبت رو با هم جمع کردم و جملات منفی رو هم با هم. سپس نشون دادم که قدر مطلق مجموع جملات منفی، نصف مجموع جملات مثبته. پس حاصل کل برابر میشه با نصف مجموع جملات مثبت.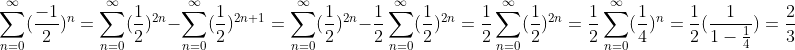
امیدوارم متوجه شده باشین.اگه نشدین بگین تا بیشتر توضیح بدم.
موفق باشین.
90/10/24




.gif)


.gif)
.gif)
.gif)
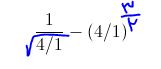
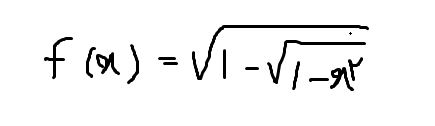

.gif) خداییش دیگه دستم از تایپ کردن خسته شد)
خداییش دیگه دستم از تایپ کردن خسته شد)