من فقط تو اون صفحه سوال اول رو ديدم برا من بقيش نبود سفيد بود
خب حالا حل سوال اول:
چون مشتق پذيره پس پيوستست:
من فقط تو اون صفحه سوال اول رو ديدم برا من بقيش نبود سفيد بود
خب حالا حل سوال اول:
چون مشتق پذيره پس پيوستست:
با سلام ...
سوال 2- خوب باید نمودار رو در قطبی ترسیم کنی باید یهزاویه های مختلف بدی و r رو به دست بیاری . بعد هم نمودار رو بکشی . حالا نمیدونم روش دقیقتری هم باشه با نه بعد از کشیدن این جوری باید بشه :
سوال 3 -
این رو کامل بلد نیستم ولی برای این که بتونی مساحت محصور بین دو تا نمودار رو به دست بیاری اولین کاری که باید بکنی این هست که نقاط تلاقی دو نمودار رو پیدا کنی بعد هم از انتگرال معین استفاده کنی که دیکه نمیدونم این قسمتش رو چه جوری باید نوشت.gif)
بقیه اش رو بلد نیستم !
سوال 3
برای به توان رسوندن اعداد مختلط باید به حالت قطبی ببری یعنی این جوری :
پس به فرم قطبی میشه :
سوال 5 قسمت ب :
ادامه ی سوال سوم
محاسبه ی انتگرال بر حسب Y راحت تر هست
با داشتن نقاط بر خورد دو نمودار با هم روی محور Y (یعنی 0 و 2) میتونیم انتگرال رو حساب کنیم.
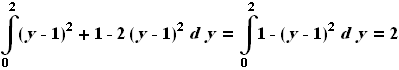
سلام.
با تشکر از جناب [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ] ولی جواب آخرش رو به نظرم درست به دست نیاوردند. در زیر مساله رو از همون روشی که ایشون حل کردند ولی با توضیحات بیشتر نوشتم.
باید ابتدا حدود یکی از x یا y رو بر حسب دیگری به دست بیاریم و حدود دومی رو به طور صریح بین دو عدد ثابت تعیین کنیم و از انتگرال دوگانه ی معین استفاده کنیم.
خب همونطور که واضحه ( و اگر هم نیست با کمی تامل واضح میشه) شکل محصور بین این دو نمودار تقریبا به صورت یه عدسی هلالی همگرا (کوژ) میشه که در دو نقطه ی
و
محصور شده و در فضای میان این دو همواره نمودار
سمت چپ نمودار
قرار میگیره. پس در فضای محصور مورد نظر میشه حدود x رو بر حسب y اینطوری در نظر گرفت:
حدود y هم که مشخصا بین صفر و 2 قرار داره. پس مساحت مورد نظر برابر با حجم منشوری با قائده ی مشخص شده (که مجهول ماست) است که ارتفاع آن منشور برابر با 1 واحد باشه:
موفق باشین.
90/10/13
Last edited by davy jones; 03-01-2012 at 20:32.
خاک پاتم حمید جان ولی خب انتگرال دوگانه ای که شما نوشتی هم داره ما رو به همون انتگرال یگانه میرسونه
البته من اون انتگرال رو اشتباه حل کردم و جواب 4/3 درسته.
با سلام ....
با تشکر از پاسخ شما .
خوب شکل با توجه به سایت ولفرام این جوری میشه :
ببخشید اصلا متوجه نشدم چرا این جوری باید بنویسیم . چرا مثلا باید اونجا توی اولین انتگرال دوگانه از عدد یک انتکرال بگیریم ؟
من اصلا متوجه نشدم منشور دیگه از کجا اومد ؟ چرا مساحت ما با حجم برابر شد ؟ اخه این که دو بعدی هست .حدود y هم که مشخصا بین صفر و 2 قرار داره. پس مساحت مورد نظر برابر با حجم منشوری با قائده ی مشخص شده (که مجهول ماست) است که ارتفاع آن منشور برابر با 1 واحد باشه:
===========================================
ببخشید میدوتم سوالم مسخره هست !من اصلا همیشه توی کاردانی هم با محاسبه این مساحت محصور بین نمودارها یا محاسبه حجم مشکل داشتم !
.gif)
به این قسمت از محاسبه که می رسیدم این جوری مشدم !
(
)
حالا هم میخوام بدونم به کتابی که این کاربردهای انتکرال رو خوب گفته باشه سراغ دارید ؟
Last edited by skyzare; 04-01-2012 at 07:45.
یه نگاهی ب این فایل میندازید؟ سه تا اثبات هسش ک بلد نیسم اثباتشونو ...
[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سلام چگونه می توان یک فرمول ریاضی fx را در کدام برنامه کامپیوتری نوشت که جوابش را بدهد
سلام دوستان عزيز اين انتگرال رو ميشه حل كنيد ممنون ميشم

سلام.
تا اینجاشو براتون نوشتم:
و اما برای حل انتگرال آخر هم ایده ای که به ذهنم رسید اینه که اگه از تغییر متغیراستفاده کنیم، زیر رادیکال میشه
ولی دیگه بعدش ایده ای به ذهنم نمیرسه
موفق باشین.
90/10/15
هم اکنون 1 کاربر در حال مشاهده این تاپیک میباشد. (0 کاربر عضو شده و 1 مهمان)