اتاق ریاضیات(طرح سؤالات)

**skyzare** · 03-12-2011, 21:18

${\color{Red} y=tan^{-1}(lnx)+ln\left ( tan^{-1}x \right )}$

$y'=\frac{\frac{1}{x}}{1+ln^{2}x}+\frac{\frac{1}{1+x^2}}{tan^{-1}x}$

$y'=\frac{1}{x(1+ln^2x)}+\frac{1}{(1+x^2)tan^{-1}x}$

**M E S S I** · 03-12-2011, 21:28

skyzare عزیز ممنونم که حداقل شما جوابمو دادید
ان شا الله خدا 1 در دنیا 100 در آخرت بهت بده...

**skyzare** · 03-12-2011, 21:51

${\color{Red} y=sin^{-1}(\frac{2x}{1+x^2})}$

$\\y(t)=sin^{-1}t\\\\ t(x)=\frac{2x}{1+x^2}$

$\frac{dy}{dx}=\frac{dy}{dt}\times \frac{dt}{dx}$

$\frac{dy}{dx}=\frac{1}{\sqrt{1-t^2}}\times \frac{2(1+x^2)-2x(2x)}{(1+x^2)^2}$

$\frac{dy}{dx}=\frac{1}{\sqrt{1-\left (\frac{2x}{1+x^2} \right )^2}}\times \frac{2(1+x^2)-2x(2x)}{(1+x^2)^2}$

$\frac{dy}{dx}=\frac{2(1-x^2)}{(1+x^2)^2\: \: \sqrt{1-\left (\frac{2x}{1+x^2} \right )^2}}$

**hts1369** · 03-12-2011, 22:25

نوشته شده توسط SuperSt@r [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سلام حالا چنتا سوال اين مدلي ديگه هم هست كه يكي ديگش رو اينجا ميذارم تا يكي يكي روش فك كنيم كه بتونيم بهتر نتيجه گيري كنيم
اگه ميشه حلش كنيد

این حد رو با چند بار استفاده از هوپیتال میشه حلش کرد.

نوشته شده توسط M E S S I [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

کسی نمی خواد جوابی بده تا حداقل دلم خوش بشه؟؟

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

میدونم زیاده حداقل 2-3 تاشو نمیتونید بگید...

من هم دو تاشون رو برات حل کردم

**skyzare** · 03-12-2011, 22:26

${\color{Red} y=\left (\sqrt{tanx} \right )^{x+1}}$

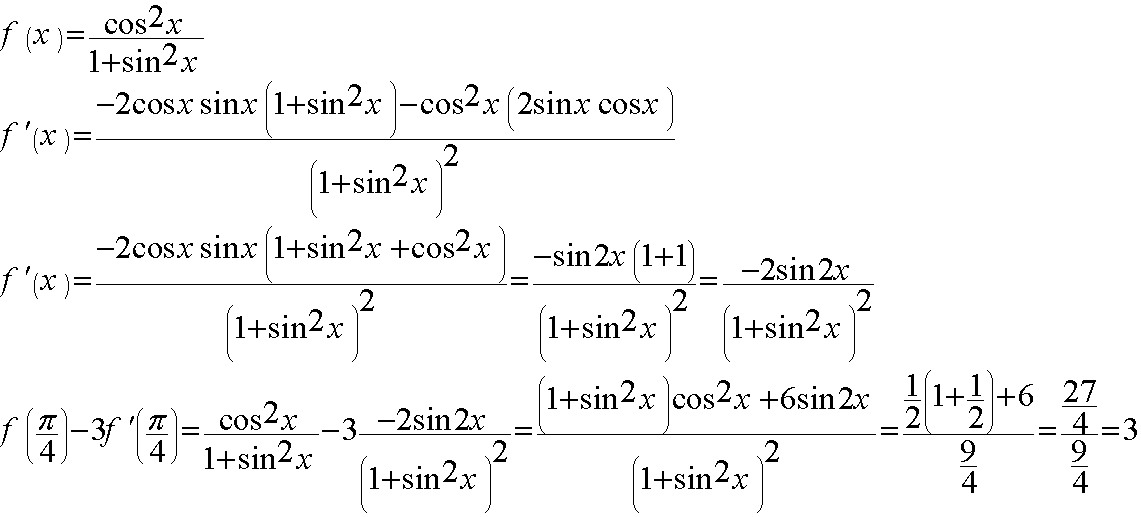
برای حل عبارت هایی که توان اون ها یه تابع بر حسب x هست باید از طرفین ln بگیریم با این کار توان به ضریب تبدیل میشه بعدش هم از طرفین نسبت به x مشتق میگیریم .

$\\ln(y)=ln(\left (\sqrt{tanx} \right )^{x+1})\\\\ ln(y)=(x+1)\times ln(\sqrt{tanx})$

حالا از طرفین نسبت به x مشتق میگیریم .

$\frac{y'}{y}=(1)ln(\sqrt{tanx})+(x+1)\frac{\frac{1+tan^2x}{2\sqrt{tanx}}}{\sqrt{tanx}}$

حالا 'y رو از این عبارت به دست میاریم .

$y'=y\left ((1)ln(\sqrt{tanx})+(x+1)\frac{\frac{1+tan^2x}{2\sqrt{tanx}}}{\sqrt{tanx}} \right )$

حالا به جای y معادلش رو میزاریم .

$y'=(\sqrt{tanx})^{x+1}\left ((1)ln(\sqrt{tanx})+(x+1)\frac{\frac{1+tan^2x}{2\sqrt{tanx}}}{\sqrt{tanx}} \right )$

**SuperSt@r** · 04-12-2011, 09:47

نوشته شده توسط hts1369 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

این حد رو با چند بار استفاده از هوپیتال میشه حلش کرد.

منم دقيقا چندبار هوپيتال گرفته بودم و يه جواب بدست اورده بودم شما اگه ميشه حداقل جواب اخر رو اينجا بذار ببينم درست حل كردم يا كه نه؟ ممنون ميشم

**skyzare** · 04-12-2011, 16:10

با سلام ...

من یه چند تا سوال ار توابع دارم .

1- دوره تناوب این دو تا تابع چیه ؟

$y=tanxcotx$

خوب حاصل این عبارت یک هست . خوب یه تابع ثابت هم متناوب هست ولی کوچکترین دوره تناوب نداره ولی توی کتابی نوشته میشه pi/2 . چرا این میشه ؟

$y=tan2x-cot2x$

خوب مگه دوره تناوب هر دوی این ها نمیشه $\frac{\pi}{2}$ که ک م م اش هم میشه همون $\frac{\pi}{2}$ دیگه ولی توی کتاب جوابش شده $\frac{\pi}{4}$

2-معکوس این تابع چی میشه ؟

$y=log_a(x+\sqrt{x^2+1})$

3-ریشه های این تابع رو چه جوری به دست میاریم ؟

$tan^{-1}\sqrt{x(x+1)}+sin^{-1}\sqrt{x^2+x+1}=\frac{\pi}{2}$

**MasterGeek** · 04-12-2011, 18:42

دوستان من یه سوال درم، فرض کنید یه بردار به این شکل رو دارین (در واقع یه سیگنال گسسته است):

$\begin{bmatrix} x(1) & x(2) & \dots & x(N+K) \end{bmatrix}$

میخوایم طی عملیاتی ریاضی به این شکل درش بیاریم:

$\begin{bmatrix} x(1) & x(2) & \dots & x(K) \\ x(2) & x(3) & \dots & x(K+1) \\ \vdots & \vdots & \vdots & \vdots \\ x(M) & x(M+1) & \dots & x(M+K) \\ \end{bmatrix}$

حالا سوال اینه چه جوری؟
اگه طی یه ضرب ساده نمیشه، آیا عملیات مشخص و خاصی رو توی جبرخطی میشناسین که خروجیش این باشه؟

**lebesgue** · 04-12-2011, 19:04

نوشته شده توسط skyzare [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

با سلام ...

من یه چند تا سوال ار توابع دارم .

1- دوره تناوب این دو تا تابع چیه ؟

$y=tanxcotx$

خوب حاصل این عبارت یک هست . خوب یه تابع ثابت هم متناوب هست ولی کوچکترین دوره تناوب نداره ولی توی کتابی نوشته میشه pi/2 . چرا این میشه ؟

$y=tan2x-cot2x$

خوب مگه دوره تناوب هر دوی این ها نمیشه $\frac{\pi}{2}$ که ک م م اش هم میشه همون $\frac{\pi}{2}$ دیگه ولی توی کتاب جوابش شده $\frac{\pi}{4}$

2-معکوس این تابع چی میشه ؟

$y=log_a(x+\sqrt{x^2+1})$

3-ریشه های این تابع رو چه جوری به دست میاریم ؟

$tan^{-1}\sqrt{x(x+1)}+sin^{-1}\sqrt{x^2+x+1}=\frac{\pi}{2}$

1. خیر، تابع ثابت 1 نیست، هر $\pi/2$ یک نقطه تعریف نشده دارد.
برای تابع دوم، توجه کنید که آن قانون ک م م فقط برای شرایط خاصی برقرار است، مثلا نمونه زیر را ببینید:

$f(x)=\sin x+(-\sin x)$

2. ابتدا ببینید:

$\left (\sqrt{x^2+1}+x \right )^{-1}=\sqrt{x^2+1}-x$

حال محاسبه کنید بر حسب x حاصل زیر را:

$e^{y}-e^{-y}=?$

3. به دامنه تابع سمت چپ معادله توجه کنید. آیا در نقطه ای به جز 0 تعریف شده است؟

**lebesgue** · 04-12-2011, 19:50

نوشته شده توسط MasterGeek [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

دوستان من یه سوال درم، فرض کنید یه بردار به این شکل رو دارین (در واقع یه سیگنال گسسته است):

$\begin{bmatrix} x(1) & x(2) & \dots & x(N+K) \end{bmatrix}$

میخوایم طی عملیاتی ریاضی به این شکل درش بیاریم:

$\begin{bmatrix} x(1) & x(2) & \dots & x(K) \\ x(2) & x(3) & \dots & x(K+1) \\ \vdots & \vdots & \vdots & \vdots \\ x(M) & x(M+1) & \dots & x(M+K) \\ \end{bmatrix}$

حالا سوال اینه چه جوری؟
اگه طی یه ضرب ساده نمیشه، آیا عملیات مشخص و خاصی رو توی جبرخطی میشناسین که خروجیش این باشه؟

من با نوتیشن های مبحث مربوطه آشنایی ندارم، اما گمان می کنم با استفاده از کانوولوشن دو بعدی (مبحث پردازش سیگنال، دستور conv2 در MATLAB) میشود.

نام تاپيک: اتاق ریاضیات(طرح سؤالات)

اختيارات تاپيک

این کاربر از skyzare بخاطر این مطلب مفید تشکر کرده است

این کاربر از M E S S I بخاطر این مطلب مفید تشکر کرده است

2 کاربر از skyzare بخاطر این مطلب مفید تشکر کرده اند

3 کاربر از hts1369 بخاطر این مطلب مفید تشکر کرده اند

این کاربر از skyzare بخاطر این مطلب مفید تشکر کرده است

سوالاتی پیرامون توابع

2 کاربر از lebesgue بخاطر این مطلب مفید تشکر کرده اند

این کاربر از lebesgue بخاطر این مطلب مفید تشکر کرده است

Thread Information

Users Browsing this Thread

User Tag List

قوانين ايجاد تاپيک در انجمن