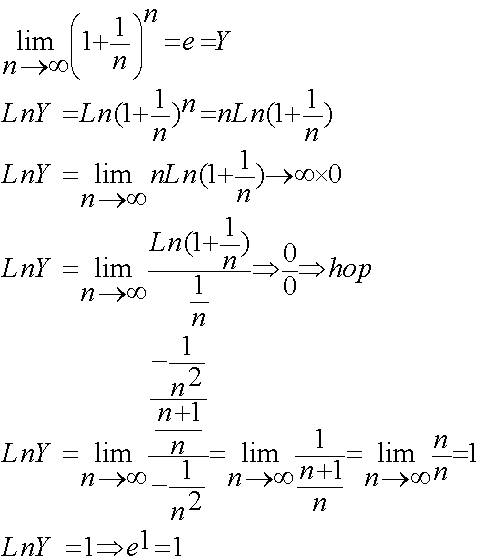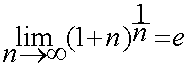اتاق ریاضیات(طرح سؤالات)

[SuperSt@r]

1-برای هر x حقیقی یک دنباله از اعداد گویا مثل q_n در نظر بگیرید که به x میل کند(چنین دنباله ای وجود دارد،چرا؟) داریم:



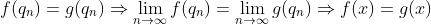
که در نتیجه گیری اخر از پیوستگی f , g استفاده شده است.

2-فرض می کنیم دامنه توابع ما بازه باشن یا کل R ...
فرض کنید چنین تابعی وجود دارد x را یک مقدار در برد این تابع در نظر بگیرید،پس a,b وجود دارند که f(a)=f(b)=x و a<b . چون f پیوسته است،پس ماکسیمم مقدار خود را روی [a,b] در نقطه ای مثل c میگیرد.و f(c)>x .
حال باید یک نقطه دیگر مثل d موجود باشد که f(d)=f(c)l.(اینجا اگه شکل تابع رو در نظر بگیرین میبینین که d چه خارج [a,b]باشه چه داخلش با توجه به پیوسته بودن نمودار باعث میشه بعضی از مقادیر بیشتر از دوبار گرفته بشن!)
اگر d خارج از [a,b] باشه و مثلا d>b:
با استفاده از قضیه مقدار میانی روی بازه [b,d] برای هر t که f(b) < t < f(c)=f(d)l عدد حقیقی s وجود دارد که f(s)=t همچنین با بکاربردن مقدار میانگین روی بازه های [a,c] , [c,b] دو مقدار دیگر مثل s بدست می اید که f(s)=t باشد پس مقدار t را تابع f حداقل سه بار میگیرد که تناقض است.
حالت d داخل بازه [a,b] باشه هم تقریبا مشابه حل میشه.
برای قسمت دوم مساله هم نمودار چنین تابعی رو معرفی میکنیم!
حرف انگلیسی N رو در صفحه مختصات بنویسید!(البته N ای که یکم مایل باشه،نه قاِئم!)
از نقطه انتهایی شمال شرقی این N یک N دیگه بنویسید و این روندو ادامه بدین...همینطور انتهای جنوب غربی این N یک N دیگه بزارین و ادامه بدین...این نمودار تابعی رو نشون میده که پیوستست،با دامنه R وهر مقدار حقیقی رو دقیقا سه بار می گیره!البته میشه ضابطه هم براش بدست اورد...

سلام دوست عزیز خیلی خیلی ازت ممنونم به خاطر اینکه وقت گذاشتی و جوابم رو دادی
اگه میشه سوال اول رو بیشتر توضیح بده آخه قشنگ متوجه نشدم
ولی سوال دوم رو گرفتم دستت درد نکنه ولی قسمت دوم که گفته هر مقدار از بردش رو سه بار اختیار کنه که ما اگه تابع N رو بکشیم و این روند رو ادامه بدیم نقاطی هستند که بیش از سه بار و حتی بیشتر هم تکرار میشن حتی شما اگه همون خود N رو به تنهایی در نظر بگیریم نقاطی هستن که سه بار بردشون یکیه چه برسه که این روند رو ادامه بدیم

در ضمن میشه نرم افزاری رو که خودتون برا نوشتن توابع و مسائل ریاضی استفاده میکنید رو معرفی کنید که اگه بازم سوالی داشتم با اون نرم افزار به راحتی بنویسمش ممنون میشم

[lebesgue]

برای قسمت دوم مساله هم نمودار چنین تابعی رو معرفی میکنیم!
حرف انگلیسی N رو در صفحه مختصات بنویسید!(البته N ای که یکم مایل باشه،نه قاِئم!)
از نقطه انتهایی شمال شرقی این N یک N دیگه بنویسید و این روندو ادامه بدین...همینطور انتهای جنوب غربی این N یک N دیگه بزارین و ادامه بدین...این نمودار تابعی رو نشون میده که پیوستست،با دامنه R وهر مقدار حقیقی رو دقیقا سه بار می گیره!البته میشه ضابطه هم براش بدست اورد...

یک نمونه برای ضابطه چنین تابعی، هست و نمودارش به صورت زیر:

a تقریباً 0.2172 بوده و به طور دقیق، ریشه معادله زیر است:

همچنین نسخه فشرده (کراندار) آن:

کسی میتواند بگوید نمودار بالا چگونه بدست آمده و ضابطه تابع آن چیست؟

[ali_hp]

سلام دوست عزیز خیلی خیلی ازت ممنونم به خاطر اینکه وقت گذاشتی و جوابم رو دادی
اگه میشه سوال اول رو بیشتر توضیح بده آخه قشنگ متوجه نشدم
ولی سوال دوم رو گرفتم دستت درد نکنه ولی قسمت دوم که گفته هر مقدار از بردش رو سه بار اختیار کنه که ما اگه تابع N رو بکشیم و این روند رو ادامه بدیم نقاطی هستند که بیش از سه بار و حتی بیشتر هم تکرار میشن حتی شما اگه همون خود N رو به تنهایی در نظر بگیریم نقاطی هستن که سه بار بردشون یکیه چه برسه که این روند رو ادامه بدیم

در ضمن میشه نرم افزاری رو که خودتون برا نوشتن توابع و مسائل ریاضی استفاده میکنید رو معرفی کنید که اگه بازم سوالی داشتم با اون نرم افزار به راحتی بنویسمش ممنون میشم

سلام،خواهش می کنم.
خوب کجاشو متوجه نشدی شما؟اول از این استفاده شد که به هر عددی با اعداد گویا میشه میل کرد،بعد هم با توجه به پیوستگی، حد f یک دنباله برابر f حد دنباله میشه...شاید اینجوری واضح تر باشه.


سوال دوم هم فکر کنم شما متوجه ساختار نمودار نشدین، شبيه نموداری که دوستمون 1233445566
گفتن ، که البته نمودار ایشون هم ضابطه داره هم برای حالت کراندارش جوابو گفتن.
برای فرمول نویسی هم میتونین اینجا رو ببینین:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

[SuperSt@r]

سلام،خواهش می کنم.
خوب کجاشو متوجه نشدی شما؟اول از این استفاده شد که به هر عددی با اعداد گویا میشه میل کرد،بعد هم با توجه به پیوستگی، حد f یک دنباله برابر f حد دنباله میشه...شاید اینجوری واضح تر باشه.


سوال دوم هم فکر کنم شما متوجه ساختار نمودار نشدین، شبيه نموداری که دوستمون 1233445566
گفتن ، که البته نمودار ایشون هم ضابطه داره هم برای حالت کراندارش جوابو گفتن.
برای فرمول نویسی هم میتونین اینجا رو ببینین:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

بازم ازت ممنونم دوست عزیز
دقیقا همین دنباله ها رو متوجه نمیشم که گفتید

برای هر x حقیقی یک دنباله از اعداد گویا مثل q_n در نظر بگیرید که به x میل کند(چنین دنباله ای وجود دارد،چرا؟)

و

اول از این استفاده شد که به هر عددی با اعداد گویا میشه میل کرد

در مورد اون تابع هم آره شکلش رو درست متوجه نشده بودم که بعدش که فک کردم متوجه شدم الانم که اون تابع با ضابطه اش رو دیدم دیگه بهتر شد

[MasterGeek]

نوشته شده توسط MasterGeek
بازم به نظرم ممکن نیست هنوز مگر اینکه شرط اینکه یکنوا بودن رو هم اضافه کنید....
چون مثلا در بازه.ی 0 تا 1 تابع زیر رو در نظر بگیرید:



پس من شرط یکنوا بودن رو اضافه میکنم:
این قضیه


پس باید در این صورت معادله.ی f(c)=c باید جوابی در بازه.ی a,b داشته باشد. چون تابع f یکنواست پس حتما خط y=c تابع f رو قطع میکنه...
اثبات رسمی تر این قضیه فکر کنم همون قضیه رول میشه یا همچین چیزی.....

البته شرط پیوسته بودن هم به طور ضمنی میشه در یکنوائی جاش داد....

سلام
مثالي كه شما زدي بازه صفر و يك به خودش تصوير نمي كنه، مثلا f(0)=2
و ٢ در بازه صفر و يك نيست.
نيازي به شرط يكنوايي هم نيست.
اين قضيه رو با به كار بردن قضيه مقدار مياني براي تابع f(x)-x روي بازه [a,b] ميشه ثابت كرد.

درسته
اما اون تابعی که نوشتم کلیتش مصداق داره (تعریفش رو اشتباه کرده بودم ولی میشه از 1 شروع بشه تغییری در کلیت مثال نقض نمیده)

صورت سوال هم از اول اشکال داشت مثلا شرط یکنوائی ولو لازم نباشد ولی لازم هست که تابع در کل بازه مشتق پذیر باشه...(که یه درجه بالاتر از پیوستگی هست)

اما درست تر همون فرضهائی بود که شما کردین....

[ali_hp]

بازم ازت ممنونم دوست عزیز
دقیقا همین دنباله ها رو متوجه نمیشم که گفتید

برای هر x حقیقی یک دنباله از اعداد گویا مثل q_n در نظر بگیرید که به x میل کند(چنین دنباله ای وجود دارد،چرا؟)

دنباله های زیادی با این خاصیت وجود دارد،مثلا می توانید بسط اعشاری x در مبنای 10 را در نظر بگیرید ، q_0 را برابر با ارقام قبل از ممیز x بگیرید ، q_1 را برابر تقریب x تا یک رقم اعشار بگیرید، q_2 را برابر تقریب x تا دو رقم اعشار بگیرید و ....مثلا اگر x=π باشد دنباله q_n بصورت زیر می شود:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

که یک جمله عمومیش میشه:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

[mofidy1]

با سلام

دوستان عزیز روی حل معادله ی زیبای زیر فکر کنید. هدف به دست آوردن تمام ریشه ها ی حقیقی و مختلط آن است ( البته بدون استفاده از نرم افزارهای ریاضی!!). روی روش های مختلف حل آن هم بحث کنید. آیا می توان از این مساله، یک روش کلی برای حل معادلات مشابه دیگر به دست آورد؟

با تشکر

19 آبان 1390

[MasterGeek]

با سلام

دوستان عزیز روی حل معادله ی زیبای زیر فکر کنید. هدف به دست آوردن تمام ریشه ها ی حقیقی و مختلط آن است ( البته بدون استفاده از نرم افزارهای ریاضی!!). روی روش های مختلف حل آن هم بحث کنید. آیا می توان از این مساله، یک روش کلی برای حل معادلات مشابه دیگر به دست آورد؟

با تشکر

19 آبان 1390

من فقط یه استراتژی واسه حلش دارم و اون از طریق پارامترهای مجهول و معادل گرفتن ضرب فاکتورهای ممکن هست. فقط مشکل اینکه باید اینا رو از روی خود معادله بفهمیم (یادمه یه روشی برای این کار وجود داشت):

1. تعداد ریشه های حقیقی معادله
2. تعداد ریشه های مکرر معادله (به خصوص اگه مختلط مکرر باشند)

اگه اینا رو بفهیم اونوقت با روش ضرائب مجهول شاید حل بشه...

[SuperSt@r]

سلام دوستان من این سوال رو روش فکری نکردم فقط حالا که دیدم اینجام گفتم که اینجا وارد کنم ببینم شما چه جوری حلش میکنید که اگه خودم حلش کردم با راه شما چک کنم البته فک میکنم ساده باشه
گفته نشان دهید

[hts1369]

سلام دوستان من این سوال رو روش فکری نکردم فقط حالا که دیدم اینجام گفتم که اینجا وارد کنم ببینم شما چه جوری حلش میکنید که اگه خودم حلش کردم با راه شما چک کنم البته فک میکنم ساده باشه
گفته نشان دهید

حلش رو برات گذاشتم
اولش بینهایت در صفر رو به صفر بر صفر تبدیل میکنیم و بعدش از hop استفاده میکنیم

این یکی رو هم بعنوان تمرین خودت حل کن (مثله قبلی هست)