اتاق ریاضیات(طرح سؤالات)

**msm43njn** · 17-02-2011, 23:43

نوشته شده توسط mohsen_blid [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

دوستان سایتی رو میدید که انتگرال رو خودش بگیره و بیشتر مسیر رو بنویسه
همچنین در رابطه با سری همگرا و واگرا

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

با راه حل کامل به انگلیسی

**davy jones** · 17-02-2011, 23:53

نوشته شده توسط mohsen_blid [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

دوستان سایتی رو میدید که انتگرال رو خودش بگیره و بیشتر مسیر رو بنویسه
همچنین در رابطه با سری همگرا و واگرا

سلام. در مورد انتگرال (انتگرال نامعین) بنده سایت زیر رو میشناسم که جواب آخر رو محاسبه میکنه. البته برای مشاهده ی مسیر راه حل به صورت گام به گام باید عضو پولی این سایت بشین. برای اعضای عادی فقط جواب آخر رو نشون میده و راه حل رو نشون نمیده:

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

البته در مورد انتگرال و همچنین سریها (به طور کلی هر مبحث مربوط به ریاضیات) سایت زیر هم به شدت توصیه میشه به دوستان. خود من به شخصه خیلی باهاش حال میکنم. کافیه تابع یا سری و یا دنباله مد نظرتون رو در کادر اصلی وسط صفحه تایپ کنید و سپس هر آنچه که ممکنه در مورد این تابع بهش احتیاج پیدا کنین براتون محاسبه میکنه. در انتهای صفحه گزینه ی Try again with more time رو انتخاب کنین تا باز هم اطلاعات بیشتری در اختیارتون بذاره:

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

موفق باشین.
89/11/28

**hadi2222** · 18-02-2011, 09:08

نوشته شده توسط afshin b [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

جواب سوال دومتون:

$A=\int \frac{dx}{x^2+a^2}=\frac{1}{a^2}\int \frac{dx}{(\frac{x}{a})^2+1}$
$\frac{x}{a}=u\Rightarrow dx=adu$
$\Rightarrow A=\frac{1}{a^2}\int \frac{adu}{u^2+1}=\frac{1}{a}arctan(u)+c=\frac{1}{a}arctan(\frac{x}{a})+c$

سلام
ممنونم
فقط اگه میشه بگید اون قسمت اخر انتگرال رو چطوری حل کردین؟(منظورم روال حل انتگرال اخر هست که به جواب نهایی میرسه که بعد از بدست اوردن اون U رو جایگرین کردین)

**afshin b** · 18-02-2011, 10:01

نوشته شده توسط hadi2222 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سلام
ممنونم
فقط اگه میشه بگید اون قسمت اخر انتگرال رو چطوری حل کردین؟(منظورم روال حل انتگرال اخر هست که به جواب نهایی میرسه که بعد از بدست اوردن اون U رو جایگرین کردین)

این یه فرموله:
$\int \frac{du}{u^2+1}=arctan(u)$

**davy jones** · 18-02-2011, 10:52

نوشته شده توسط hadi2222 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سلام
ممنونم
فقط اگه میشه بگید اون قسمت اخر انتگرال رو چطوری حل کردین؟(منظورم روال حل انتگرال اخر هست که به جواب نهایی میرسه که بعد از بدست اوردن اون U رو جایگرین کردین)

نوشته شده توسط afshin b [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

این یه فرموله:
$\int \frac{du}{u^2+1}=arctan(u)$

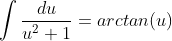
بفرمایین اینم اثبات فرمولش:

همونطور که از فرمول مشتق زنجیره ای میدونیم داریم:

$[{f(g(x))}]'={g}'(x){f}'(g(x))$

در نتیجه داریم:

$f^{-1}(f(x))=arctan(\tan (x))\equiv x\Rightarrow {[arctan(\tan (x))]}'={[x]}'\Rightarrow (1+\tan ^{2}(x)){[{arctan}'(\tan (x))]}=1\Rightarrow {arctan}'(\tan (x))=\frac{1}{1+\tan ^{2}(x)}\Rightarrow {\color{red} {arctan}'(x)=\frac{1}{1+x^{2}}}$

$\Rightarrow \int \frac{dx}{1+x^{2}}=arctan(x)+c$

موفق باشین.
89/11/29

**hojjatinho** · 22-02-2011, 21:21

سلام
می دونیم که برای رفع ابهام بینهایت درصفر می تونیم ان رو به شکل 0/0 یا بینهایت بر بینهایت در اوریم سوال اینجاست که چگونه از همان اول بدونم از کدوم یکی استفاده کنم؟
با تشکر

**davy jones** · 22-02-2011, 21:53

نوشته شده توسط andre22 [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سلام
می دونیم که برای رفع ابهام بینهایت درصفر می تونیم ان رو به شکل 0/0 یا بینهایت بر بینهایت در اوریم سوال اینجاست که چگونه از همان اول بدونم از کدوم یکی استفاده کنم؟
با تشکر

سلام.
در این زمینه همواره نمیشه با قاطعیت جواب داد. بستگی به مساله اش داره. هر وقتی باید از حالتی که کارمونو راحت تر میکنه و ابهام راحت تر برطرف میشه استفاده کرد.

موفق باشین.
89/12/3

**mohsen_blid** · 22-02-2011, 21:55

سلام خدمت دوستان
من در قسمت قرمز رنگ دچار مشکلم میشه یکی راهنمایی کنه منظورم 1/3 هست

در جای دیگه اپلود کردم

اینجا هم می تونید ببینید

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

**ask_bl** · 22-02-2011, 22:00

نوشته شده توسط mohsen_blid [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سلام خدمت دوستان
من در قسمت قرمز رنگ دچار مشکلم میشه یکی راهنمایی کنه منظورم 1/3 هست

سلام
عکسا که برا من لود نشدن !

**davy jones** · 22-02-2011, 22:32

نوشته شده توسط mohsen_blid [ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

سلام خدمت دوستان
من در قسمت قرمز رنگ دچار مشکلم میشه یکی راهنمایی کنه منظورم 1/3 هست

در جای دیگه اپلود کردم

اینجا هم می تونید ببینید

کد:

برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید

سلام.

بفرمایید:

$\lim_{n \to \infty }\frac{n(n+1)(2n+1)}{6n^{3}}=\lim_{n \to \infty }\frac{2n^{3}+3n^{2}+n}{6n^{3}}\; \equiv \lim_{n \to \infty }\frac{2n^{3}}{6n^{3}}=\frac{2}{6}=\frac{1}{3}$

البته دقت داشته باشین چون حد به سمت بینهایت هستش ما میتونیم از جملات با درجه ی کمتر در صورت کسر صرفنظر کنیم. در حالت غیر از بینهایت چنین کاری صحیح نیست.

این مثالی که نوشتین مربوط به قضیه انتگرال ریمان برای تابع y=x^2 هستش.

موفق باشین.
89/12/3

نام تاپيک: اتاق ریاضیات(طرح سؤالات)

اختيارات تاپيک

این کاربر از msm43njn بخاطر این مطلب مفید تشکر کرده است

این کاربر از davy jones بخاطر این مطلب مفید تشکر کرده است

4 کاربر از afshin b بخاطر این مطلب مفید تشکر کرده اند

5 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

2 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

3 کاربر از davy jones بخاطر این مطلب مفید تشکر کرده اند

Thread Information

Users Browsing this Thread

User Tag List

قوانين ايجاد تاپيک در انجمن