ماهان سرور
آکوستیک ، فوم شانه تخم مرغی ، پنل صداگیر ، یونولیت
دستگاه جوجه کشی حرفه ای
فروش آنلاین لباس کودک
خرید فالوور ایرانی
خرید فالوور اینستاگرام
خرید ممبر تلگرام
[ + افزودن آگهی متنی جدید ]
با عرض سلام
ابتدا اینکه اگه سوالمو جای نامناسبی مطرح میکنم از همگی عذار میخوام هرچقدر دنبال گشتم تاپیکی که مربوط به سوالم بشه رو پیدا نکردم
اما سوالم از دوستان عزیز اینه:
لطفا اثبات فرمول مدول برشی قانون هوک (مدول برشیGو vضریب پواسون) رو بصورت کامل بذارید
G=E/2 (1+v
با تشکر
Last edited by hamid1002; 09-11-2012 at 07:49.
سلام
متاسفانه من اطلاعاتی در این زمینه ندارم اما لینک زیر رو پیدا کردم ببینید به دردتون می خوره :
کد:برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید
ممنون دوست عزیز ولی من بصورت کاملشو میخوام این اخرشو اینقدر تند رفته که نمیشه متوجه شد
دوستان ممنون میشم همرسی میانه ها و ارتفا هارو واسم اثبات کنید من که الان 1ساعته دارم فک میکنم:|لطفا امروز ج بدید فردا امتحان دارام
چرا وقتی دو متغیر تصادفی مستقل اند هرترکیبی از اون ها با یکیشون مستقل اند چرا وقتی دو متغیر تصادفی مستقل اند هرترکیبی از اون ها با یکیشون مستقل اند؟؟؟
Sent from my GT-I9100 using Tapatalk 2
اگه کسی میتونه به اینا جواب بده ممنون میشم
الف( اگر صفحه را با سه رنگ مختلف رنگ کنیم، ثابت کنید دو نقطهی همرنگ با فاصلهی 1 وجود دارند.
ب( اگر فضا را با چهار رنگ مختلف رنگ کنیم، ثابت کنید دو نقطهی همرنگ با فاصلهی 1 وجود دارند.
اگه تونستین سریع لطفا
بی زحمت کسایی که هستن اگه میتونن جواب مارو بدن
Last edited by armanassassin; 08-12-2012 at 23:53.
سلام
یه سوال ابتدایی دارم از هندسه ،ممنون میشم جواب بدید.
ثابت کنید در هر مثلث متساوی الساقین :
الف)دو زاویه مربوط به ساق ها با هم برابرند
ب)ارتفاع،میانه،عمودمنصف و نیمساز در مثلث نتساوی الساقین به هم منطبق اند
ممنون
سلام و درود بر شما
من یه سوال دارم ک برای درس مبانی هندسه دانشگاهه
البته ااین موضوع ب عنوان راهنمایی برای حل یه سوال دیگه مطرح شده ولی من قادر ب حلش نیستم
در واقع نمیدونم چطوری میشه یک به یک بودن این رو حساب کرد در صورتی ک دوتا متغیر داره یعنی باید یک ب یک بودن تابع زیر رو بررسی کنیم.
ممنون میشم اگر راهنمایی کنید.
سلامسلام و درود بر شما
من یه سوال دارم ک برای درس مبانی هندسه دانشگاهه
البته ااین موضوع ب عنوان راهنمایی برای حل یه سوال دیگه مطرح شده ولی من قادر ب حلش نیستم
در واقع نمیدونم چطوری میشه یک به یک بودن این رو حساب کرد در صورتی ک دوتا متغیر داره یعنی باید یک ب یک بودن تابع زیر رو بررسی کنیم.
ممنون میشم اگر راهنمایی کنید.
من یک به یک بودن رو برای توابع دو متغیره نشنیدم . یه نگاهی هم توی اینترنت انداختم چیزی پیدا نکردم .
به شکل زیر توجه کنید :
کد متمتیکا :
اینو می شه واقعا گفت یک به یکه ؟ دلیل این که یه معیار رسمی برای قضاوت در مورد یک به یک بودن توابع دو متغیره نداریم اینه که معرفی « یک به یک بودن » برای توابع با بیش از یک متغیر تعمیم تعریف یک به یک بودنه . بنابراین شاید بشه گفت تابعی یک به یکه که به ازای هر مقدارش فقط و فقط یک نقطه متناظر باهاش از صفحات موازی با x-y وجود داشته باشه . یا به عبارت ساده تر هر صفحه ی موازی با صفحه ی x-y ، نمودار تابع رو فقط در یک نقطه قطع کنه که نمی کنه (مطابق شکل)کد:برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید
جایی هم دیدم نوشته بود :
در هر حال وقتی کسی تعریفی رو تعمیم می ده شاید بهتر باشه اونو بازنویسی کنه .
شما خواستین سوالو بزارین شاید بهتر بشه کمک کرد.
سوال1:
گزاره "خطوط موازی یکدیگر را در بینهایت قطع میکنند" را در هر سه مدل معرفی شده در این بخش توضیح دهید .در صفحه پوانکاره و یا کره ریمان کلمه "در بینهایت " معنی دارد؟
سوال 2
ثابت کنید:
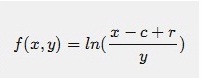
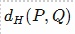در حالت
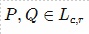در شرط دوم تعریف d صدق میکند.
در واقع جواب هر دو سوال به راهنمایی ک قبلا خواستم مربوط میشه
تا جایی ک من میدونم برای اثبات یک ب یک بودن f(x,y)f باید c , r را ثابت فرض کنیم و بعد یک ب یک بودنش رو اثبات کنیم.
هم اکنون 1 کاربر در حال مشاهده این تاپیک میباشد. (0 کاربر عضو شده و 1 مهمان)
قوانين ايجاد تاپيک در انجمن
جواب بصورت نقل قول
نوشته شده توسط hamid1002
