◄◄ اتــــاق آمــــار و احــــتــــمــــال ►►

[taghi_ramzi]

سلام

عذر میخوام اگه سوالام یه کم مبتدیه.

امید ریاضی اومدن یه عدد خاص توی تاس چطور حساب میشه؟ کل کتاب دکتر نعمت اللهی رو گشتم ، مثال امید ریاضی مربوط به تاس توش نبود

سوال دیگه م اینه که تتا در توزیع نمایی چیه ؟ تو کتاب نعمت اللهی صفحه ی 195 چرا مجدداً تتا رو گذاشته تو تابع چگالی احتمال؟

[davy jones]

سلام.

نمونه سوال امتحان میان ترم درس آمار و احتمال دانشگاه غیرانتفاعی غیاث الدین جمشید کاشانی در همین ترم جاری رو به همراه حلش برای همه ی دوستان قرار میدم:

لینک تصویر صورت سوالها:

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

جوابهایی که خودم نوشتم.

  محتوای مخفی: کلیک کنین 

سوال یک:
اول 4 تا محل کار رو از 11 تا انتخاب میکنیم که سبزشون کنیم. به چند روش میشه انتخاب کرد؟ (جواب: ) حالا میمونه 7 تا محل کار که هنوز رنگ نشدن. اینبار 3 تا از اینا رو انتخاب میکنیم که زردشون کنیم. به چند روش امکان داره؟ (جواب: ) حالا مونده 4 تا محل کار که هنوز رنگ نشدن. 2 تاشون رو برای رنگ سفید انتخاب باید بکنیم. چند حالت داره (جواب: ) حالا 2 محل کار مونده که باید صورتی بشه. 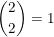به چند حالت میشه 2 محل کار رو از 2 محل کار باقیمونده برای رنگ صورتی زدن انتخای کرد؟ (جواب: ) پس جواب کلی میشه:




=========================================

سوال دو:

اول باید تعداد حالات انتخاب پیشامد مطلوبمون رو حساب کنیم و سپس این مقدار رو به تعداد کل حالات تقسیم کنیم تا احتمال مطلوب به دست بیاد.

خب حالا به چند روش میتونیم 3 مرد رو از میان 6 مرد انتخاب کنیم. (جواب: ) همچنین به چند روش میتونیم 2 زن رو از میون 9 تا زن انتخاب کنیم؟ (جواب: ) پس تعداد کل حالات پیشامد مطلوبمون میشه:

حالا تعداد حالاتی که میشه به طور کلی یک شورای 5 نفره رو از میان 15 نفر حاضر انتخاب کرد چقدره؟ (جواب: ) پس جواب کلی این سوال هم میشه:



======================================

سوال سه:
فرض میکنیم که تعداد زن ها و مرد ها (که در صورت سوال گفته تعداد هر کدوم از این دسته ها برابر اونیکی هستش) برابر با x باشه. پس تعداد مردهای کور رنگی دار برابر میشه با



و تعداد زن های کور رنگی دار میشه:



بنابراین نسبت تعداد مردهای کور رنگ، به زنهای کور رنگ، میشه:



پس یعنی احتمال اینکه یک مرد را که کور رنگی داره انتخاب کنیم 20 برابر یک زن کور رنگی دار هستش. پس جواب این مساله میشه:



===============================

سوال چهار:

نقیض این مساله (که بهش متمم احتمالاتی هم میگن) میشه اینکه بگیم:
در آزمایش 4 بار پرتاب یک سکه سالم احتمال اینکه حتی یک مرتبه شیر هم ظاهر نشود چقدر است؟
اگه مقدار احتمال سوال اصلی رو با مقدار احتمال این سوال جدید با هم جمع کنیم چی میشه؟ مطمئنا جواب برابر با 1 میشه چون در 4 بار پرتاب یک سکه حتما یکی از این دو حالت رخ میده و حالت سومی هم وجود نداره:
یا حداقل یک شیر ظاهر میشه --- یا اصلا یه دونه شیر هم نمیاد.
پس مجموع این دو احتمال، کل فضای نمونه رو پوشش میده.

حالا این به چه دردمون میخوره؟ محاسبه ی جواب سوال دومی که من طرح کردم و در حقیقت متمم سوال اصلیه به مراتب راحت تر از حل سوال اصلیه. وقتی جواب متمم رو حساب کردیم، مقدار یک رو منهای جواب به دست اومدمون میکنیم و به جواب اصلی میرسیم. (کلا تو هر سوالی عبارت دست کم یا حداقل یا چیزایی شبیه به اینا رو دیدین شک نکنین که راحت ترین که از این راه برین. منتها باید متمم شرایط مساله رو درست نشخیص بدین)

حالا میریم سراغ حل این سوال که در آزمایش 4 بار پرتاب یک سکه سالم احتمال اینکه حتی یک مرتبه شیر هم ظاهر نشود چقدر است؟

خب یعنی باید هر 4 بار خط بیاد که احتمالش برابر میشه با . پس جواب کلی مساله میشه:



===============================

سوال پنج:

از قاعده ی زنجیره ای میریم. یعنی اول احتمال انتخاب شدن دسته ی اول و بعدش احتمال انتخاب شدن 3 کارت قرمز از این دسته. بعدش هم همین محاسبه رو با دسته ی دوم انجام میدیم. و در نهایت حاصل هر کدوم از دو دسته رو با هم جمع میکنیم (چون انتخاب شدن دسته ی اول یا دوم مستقل از هم نیستند و اگه هر کدوم انتخاب بشه دیگه یعنی اون یکی دسته انتخاب نشده. اگه انتخاب دو دسته از هم مستقل بود جوابها باید در هم ضرب میشد)

دسته ی اول:
احتمال انتخاب شدن این دسته:
احتمال انتخاب شدن 3 کارت قرمز از مجموع 6 کارت قرمز و 5 کارت آبی موجود در این دسته:

دسته ی دوم:

احتمال انتخاب شدن این دسته:
احتمال انتخاب شدن 3 کارت قرمز از مجموع 9 کارت قرمز موجود در این دسته:

پس جواب کلی مساله میشه:



===========================

سوال شش:

تعداد خالها در تاس برابر با مقدار عدد اون وجه تاس هستش و مساله به زبون ساده تر میشه اینکه بگیم در پرتاب دو تاس احتمال اینکه مجموع 8 ظاهر شود ولی جفت 4 نیامده باشد کدام است؟

کل حالاتی که منجر به مجموع 8 میشه عبارته از: 2و6 ، 6و2 ، 3و5 ، 5و3 (جفت 4 هم که قبول نیست) پس کلا تعداد حالات پیشامد مطلوبمون میشه 4 تا حالت. حالا باید این مقدار رو بر تعداد کل فضای نمونه ایمون (که پرتاب دو تاس در حالت کلی هستش) تقسیم کنیم تا احتمال مطلوب به دست بیاد:

پی نوشت: چقدر درسا امروزه گلابی و ساده شده. زمان ما پوستمونو میکندن تو درس آمار و احتمال!


موفق باشین.
90/10/20

[davy jones]

تکراری شد. لطفا حذف شود.

[ali_hp]

سلام

عذر میخوام اگه سوالام یه کم مبتدیه.

امید ریاضی اومدن یه عدد خاص توی تاس چطور حساب میشه؟ کل کتاب دکتر نعمت اللهی رو گشتم ، مثال امید ریاضی مربوط به تاس توش نبود

سوال دیگه م اینه که تتا در توزیع نمایی چیه ؟ تو کتاب نعمت اللهی صفحه ی 195 چرا مجدداً تتا رو گذاشته تو تابع چگالی احتمال؟

سلام
سوال اولتون مبهمه!ولی فکر کنم منظورتون اینه:
امید ریاضی عدد ظاهر شده در پرتاب یک تاس چقدره؟
جواب:
برای محاسبه امید ریاضی باید مقادیر ممکن را در احتمال وقوع متناظر هر مقدار ضرب کرده و نتایج را جمع کنیم.

من کتاب نعمت اللهی رو ندارم،و سوالتونم دقیقا نفهمیدم،ولی معمولا پارامتر مرتبط با توزیع نمایی برابر متوسط تعداد پیشامدهاست.و لاندا نامیده میشود.و طبیعتا لاندا در تابع توزیع و چگالی متغیر تصادفی نمایی هم ظاهر می شود.(تابع چگالی مشتق تابع توزیع است)
تتا میانگین توزیع نماییه..تعبیر اون متوسط فاصله زمانی بین دو پیشامد ه .تتا برابر معکوس لاندا است!
پس تابع چگالی و توزیع این متغیر تصادفی بر حسب تتا هم قابل بیان هستند...

[saadat68]

سلام دوستان

یک مدلی هست توی بحث پیشبینی و احتمالات مثل پیشبینی فوتبال یا مسائل دیگه که فرمولش رو در این 6 صفحه توضیح داده من انگلیسی زیاد خوب نیست و ریاضی هم به کل تعطیلم

[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]

لینک مستقیم - 78 کیلوبایت

اصلا نمیفهمم چی شده ( در اخر مقاله بازی آرسنال و لیورپول رو طبق همین فرمول به صورت زیر پیشبینی کرده )


P(Arsenal win) = 0.497
P(Draw) = 0.261
P(Liverpool) = 0.236

که اگر در 100 ضرب بشه به درصد احتمال برد مساوی و باخت رو به ما میده

من میخوام بدونم چه شکلی اینا رو به دست آورد

این فرمولای ریاضیشو یکی به من توضیح میده و این که چه شکلی حساب میشه

پیشاپیش ممنون

[taghi_ramzi]

با سلام
با اعداد 0-1-2-3-4-5 چند عدد سه رقمی میشه ساخت که بر سه بخشپذیر باشه ؟
فقط فرمول رو هم بگید کافیه. با تشکر.

[davy jones]

با سلام
با اعداد 0-1-2-3-4-5 چند عدد سه رقمی میشه ساخت که بر سه بخشپذیر باشه ؟
فقط فرمول رو هم بگید کافیه. با تشکر.

سلام.
بابت دیرکرد در پاسخ گویی معذرت میخوام.
سوال جالبی بود. فکرم رو درگیر خودش کرد.

همونطور که میدونیم، همه ی اعداد حسابی به سه دسته تقسیم میشند:
الف) اونهایی که مضرب 3 هستند و میشه اونها رو به صورت 3k نوشت.
ب) اونهایی که باقیمانده ی تقسیمشون به 3 برابر با یک میشه و میتوان اونها رو به صورت 3k+1 نوشت.
ج) اونهایی که باقیمانده ی تقسیمشون به 3 برابر با دو میشه و میتوان اونها رو به صورت 3k+2 نوشت.


حالا با این توضیحات، مجموع سه عدد تنها در چهار حالت بر 3 بخشپذیر میشه:

1- هر سه عدد 3k باشند.
2- هر سه عدد 3k+1 باشند.
3- هر سه عدد 3k+2 باشند.
4- یکی از اعداد 3k باشه و یکی دیگر از اونها 3k+1 باشه و سومی هم 3k+2 باشه.

از اونجایی که در بین ارقام صفر تا 5، از هر کدام از حالتهای الف) و ب) و ج) تنها دو رقم وجود داره، پس خود به خود حالتهای 1- و 2- و 3- نمیتونن اتفاق بیفتند و فقط باید حالت چهارم اتفاق بیفته. و از اونجایی که برای انتخاب رقم اول که فرض کردیم از نوع 3k هستش، دو انتخاب دارم؛ و برای انتخاب رقم دوم از بین ارقام 3k+1 هم دو انتخاب داریم؛ و برای جایگاه سوم هم به همین استدلال دو انتخاب داریم؛ پس جواب تا اینجا میشه میشه 2*2*2 یعنی 8 حالت. و چون به 3 فاکتوریل هم میشه ارقام انتخاب شده رو جایگشت داد، پس باید !3 رو هم در 8 ضرب کنیم.

اما باید به این نکته توجه کرد که رقم صفر نمیتونه در صدگان قرار بگیره چون در اونصورت عدد ما دو رقمی میشه نه سه رقمی. پس باید حالاتی رو که رقم صفر در صدگان قرار گرفته رو هم بشماریم و از جواب به دست اومده در قسمت قبل کم کنیم.

فرض میکنیم که رقم صفر در صدگان هستش. بنابراین اونیکی رقم 3k ای رو که داشتیم (منظورم رقم 3 هستش) رو باید بندازیم دور فعلا. برای دهگان، از بین ارقام 3k+1، دو انتخاب داریم و برای یکان، از بین ارقام 3k+2 هم دو انتخاب داریم که میشه 4 حالت. اما جای یکان و دهگان رو هم میشه عوض کرد. پس دو فاکتوریل هم جایگشت یکان و دهگان رو داریم که باید در 4 ضرب بشه.

پس جواب کلی این مساله میشه:

موفق باشین.
90/10/30

[taghi_ramzi]

سلام ، با تشکر از لطف شما
من با محاسبه تو امتحان میان ترم درآورده بودم 45 ، مطمئن نبودم درست باشه ، یه برنامه کوچیک c++ نوشتم ، تعداد رو 60 نشون میده

[davy jones]

سلام ، با تشکر از لطف شما
من با محاسبه تو امتحان میان ترم درآورده بودم 45 ، مطمئن نبودم درست باشه ، یه برنامه کوچیک c++ نوشتم ، تعداد رو 60 نشون میده

سلام.
در اینجا تکرار ارقام هم مجاز شمرده شده. البته در سوال اصلی هم تکرار ارقام غیرمجاز نشده بود. بنابراین شرایط مساله رو بنده دقت نکرده بودم و به همین خاطر پوزش میطلبم. اگه تکرار ارقام مجاز باشه، اونوقت حالت های جدیدی هم اضافه خواهند شد:

مجموع 3 رقم یک عدد 3 رقمی در صورتی مضرب 3 میشن که:

الف) هر 3 رقم 3k باشن. یعنی هر 3 رقم از بین ارقام 0 و 3 انتخاب بشن: برای صدگان یک انتخاب داریم و برای دهگان و یکان، هر کدام دو انتخاب داریم. پس تعداد حالات این قسمت میشه: 4 حالت.

ب) هر 3 رقم 3k+1 باشن. یعنی هر 3 رقم از بین ارقام 1 و 4 انتخاب بشن: برای هر کدام از صدگان و دهگان و یکان، 2 انتخاب داریم. پس تعداد حالات این قسمت میشه: 8 حالت.

ج) هر 3 رقم 3k+2 باشن. یعنی هر 3 رقم از بین ارقام 2 و 5 انتخاب بشن: باز هم برای هر کدام از صدگان و دهگان و یکان، 2 انتخاب داریم. پس تعداد حالات این قسمت میشه: 8 حالت.

د) یک رقم 3k، یک رقم 3k+1 و یک رقم 3k+2 داشته باشیم: تعداد حالات این قسمت رو هم که در پست قبلی 40 حالت محاسبه کردیم.


پس ... جواب کلی میشه مجموع حالات این 4 قسمت که برابر میشه با 40+8+8+4 که برابر با همون 60 میشه.


موفق باشین.
90/10/30

[hm6111]

ﺳﺴﻼﻡ ﺧﻮﺍﻫﺶ ﻣﯿﮑﻨﻢ ﺟﻮﺍﺏ ﺍﯾﻦ ﭼﻨﺪ ﺗﺎ ﺳﻮﺍﻝ ﻣﻨﻮ ﺑﺪﯾﻦ. ﺗﯿﻤﯽ 5ﻣﺴﺎﺑﻘﻪ ﺩﺍﺭﺩ ﺍﺣﺘﻤﺎﻝ ﺑﺮﺩ ﺑﺎﺧﺖ ﻭ ﻣﺴﺎﻭﯼ ﺑﻪ ﺗﺮﺗﯿﺐ 04. ﻭ 025.ﻭ 035. ﺍﺳﺖ ﺑﺎ ﮐﺪﺍﻡ ﺍﺣﺘﻤﺎﻝ ﺍﯾﻦ ﺗﯿﻢ 3ﺑﺮﺩ ﻭ ﯾﮏ ﺑﺎﺧﺖ ﻭ ﯾﮏ ﻣﺴﺎﻭﯼ ﺩﺍﺷﺘﻪ ﺑﺎﺷﺪ ؟

ﺑﺎ ﺣﺮﻭﻑ success ﭼﻨﺪ ﺭﻣﺰ ﻋﺒﻮﺭ ﭼﻬﺎﺭ ﺭﻗﻤﯽ ﻣﯿﺘﻮﺍﻥ ﺳﺎﺧﺖ