سلام
میخواهیم که بسط مک لورن تابعرا بنویسیم. محاسبات را انجام میدیم تا برسیم به
حالا برای محاسبه مقدارو سایر مشتقات میتونیم از بسط مک لورن
که میشه
استفاده کنیم؟ مثلا:
ممنون.gif)
سلام
میخواهیم که بسط مک لورن تابعرا بنویسیم. محاسبات را انجام میدیم تا برسیم به
حالا برای محاسبه مقدارو سایر مشتقات میتونیم از بسط مک لورن
که میشه
استفاده کنیم؟ مثلا:
ممنون.gif)

سلام
سوال درست نیست،مثلا تابع ثابت F(x)=1 را در بازه [3,4] در نظر بگیرید.
سلام....آقا ما توي اين اتگرال گير كرديم!!!
نميدونم چطوري اينو نتيجه گرفته....
اينم عكسش::::


ببخشید 1 شرط رو یادم رفته بود بگذارم
F(a = F(b = 0
بازم سوال درست نیست. برای اینکه شیر فهم بشی این نکته رو همیشه بیاد داشته باش که تنها تابع غیر صفری که مشتقش با خودش برابره تابع نماییه:
y=e^x
حالا اگه تابع f با همه ی اون مشخصاتی که گفتی با این تابع حداقل یه بار برخورد کنه مساله جواب داره ولی خیلی واضحه که میشه یه تابع f مثال زد که در یک بازه (a,b) که a,b>0 هستند پیوسته و مشتقپذیر باشه و f(a)=f(b)=0 هم صادق باشه ولی با نمودار تابع نمایی تداخل نداشته باشه.
احتمالا سوال یه شرط دیگه هم داره مثلا اینکه: a<0
امیدوارم تونسته باشم منظورمو درست بگم.
موفق باشین.
88/8/3
معلومه که نیست. چون رادیکال n یه تابع اکیدا صعودیه.
موفق باشین.
88/8/3
من حوصله ی حساب کردنشو ندارم. ولی راهنمایی میکنم که یه معادله ی کلی مثل:
y=ax+b
در نظر بگیر و مجموع مربعات طول پاره خطهای عمود بر این تابع رو برای تک تک داده ها بطور پارامتری حساب میکنی. حالا این باید مینیمم بشه. یه بار نسبت به a و یه بار نسبت به b مشتق میگیری و اونا رو مساوی با صفر میذاری تا a و b مشخص بشن.
البته یه راه بسیار ساده تر هم داره اونم اینکه بری توی محیط excel و این داده ها رو وارد میکنی و میری تو قسمت نمودار کشیدن و توی اختیارات اضافه ی نمودار میتونی تعیین کنی که خود excel این کار رو بکنه. معادله خط و واریانس رو هم خودش حساب میکنه و بهت میگه.
موفق باشین.
88/8/3

شما 1 مثال نقض برای من بیار.منظور من از سوال این هست که حد اقل 1 سی وجود دارد که در شرایط مسئله صدق می کند.

با این شرط حکم برقراره...
اثبات:
طبق قضیه رل نقطه ای مثل w وجود دارد که مشتق f در w صفر شود و a<w<b .اگر f(w)=0 که w همان نقطه مورد نظر است.پس بدون کم شدن از کلیت مساله فرض کنید f(w)>0 .قرار دهید :
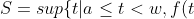=0\})
با توجه به پیوستگی f داریم f(S)=0.اگر مشتق f در S صفر باشد که S همان نقطه مورد نظر است. همچنین اگر مشتق f در S منفی باشد،با sup بودن S متناقض است.پس مشتق f در S مثبت است،حال تابع
را در بازه [S,w] در نظر بگیرید،در S منفی است و در w مثبت.پس با توجه به قضیه مقدار میانی در نقطه ای مثل c صفر می شود.

سلام،این دنباله همگرا نیست چون بیکرانه...
اگر یک دنباله اکیدا صعودی باشه نمیشه نتیجه گرفت که همگرا نیست.مثلا دنباله

اکیدا صعودیه ولی همگرا است.
Last edited by ali_hp; 26-10-2009 at 10:22.
هم اکنون 1 کاربر در حال مشاهده این تاپیک میباشد. (0 کاربر عضو شده و 1 مهمان)