1. جناب mojtabaivi برای اولین بار به بخشی از پاسخ صحیح اشاره کردند. ایشان با مدلسازی دستی (و البته دیفرانسیلی دستی) مسئله به شهود خوبی راجع به جواب نهائی رسیدند. قسمت‌های درست اشاره ایشان، کشیدن شهودی مسیر و اشاره به همزمان رسیدن حیونها به یک نقطه هست.
سر انجام این مسیر، اینه که هر 4 حیوون همزمان به هم میرسن.
ببینید در لحظه ی ابتدایی که هر کدام از حیوانها در یکی از چهار گوشه ی مربع هستند، در آغاز حرکت، جهت حرکت هر کدام منطبق بر ضلع مربع است. در لحظه ی بعدی، دیگه مسیر هر کدوم از حیوون ها، ضلع مربع نیس، چون هر حیوان به سمت دیگری حرکت کرده و مسیر حرکت هرکدوم از حیوون ها نسبت به مسیر قبل کمی زاویه گرفته. و این روند تا پایان ادامه پیدا میکنه. شکل زیر مسیر تا نصفه ی حرکته:
همونطور که معلومه، هر حیوون مسیرش به شکل یک منحنی در میاد که هر لحظه شیبش تغییر میکنه و امتداد شیبش، منطبق بر خط واصل دو تا حیوونه و در نهایت این چهار تا همزمان به هم میرسن.
چون من نتوستم شکل رو به درستی رسم کنم و با استفاده از خط کش رسم کردم و اونم به صورت 1 سانتی (یعنی هر برای هر لحظه حرکت حیوونا، یک سانت هر کدوم رو جلو بردم D
شکل نهایی رو میذارم ولی تلاش میکنم با نرم افزار بتونم درست کنم تا دقیق بشه
البته ایشون در پست بعدی یک اصلاحیه دادن و اشتباه کوچیکی که مرتکب شده بودند رو رفع کردند.
همینطور ایشون به این نکته در مورد سوال اشاره کردند:
2) یه الگوی جالبی که متوجه شدم اینه که همواره 4 حیوون روی 4 گوشه ی یک مربع هستند که این مربع به صورت ساعتگرد حول مرکزش میچرخه و هر لحظه کوچیک میشه و به سمت صفر میل میکنه
خب بنابراین حل ایشون بخش مهمی در درک شهودی مسئله بود (قدم اول) و متاسفانه با بیان ریاضی همراه نبود (قدم آخر) که سوال اصلی ما بود یعنی زمان و مسیر (حداقل با یک پارامتر مبین) حرکت به شکل ریاضی. به همین خاطر ایشون بابت این حل ۱.۵ امتیاز کسب می‌کنند.
جناب sara_program، جواب شما درست نیست متاسفانه چون با یک فرض نادرست پیش رفتید که در اینجا به قرمز نشون دادم خودبخود نتیجه‌گیری‌های متعاقب هم درست نیست. شما باید برای این فرض دلیل موجهی میداشتید.
من جوابمو اصلاح می کنم
هر 4 تا حیوان حول یک دایره در جهت ساعتگرد حرکت می کنند. در واقع چون سرعت ثابت است هر حیوان به سهم خودش مسیر را طی می کند یعنی 1/4 مسافت را طی می کند. یعنی شکل زیر
ضلع مربع d است پس نتیجه می گیریم که برای هر دایره شعاع برابر است با : r= d/2
پس محیط هم دایره می شه :
2pr = 2pd/2 = pd
هر حیوان 1/4 مسیر را طی می کند پس داریم:
pd/4
از نظر ریاضی ثابت کردیم که هر حیوان فقط موفق میشه 1/4 مسیر را طی کند. پس این یعنی اونها فقط یکبار بودن در روی گوشه مربع را تجربه می کنند و دیگر موفق نمی شوند به مربع بازگردند. یعنی همگی در راس مربع به هم می رسند.
جناب Iron در این پست:
مسیر همونیه که در پستهای 177 و 178 گفته شد (در جهت ساعتگرد) و همونطوریکه گفته شد و در شکل 1 هم نشون داده شده چهار حیوان همواره در چهارگوشه یک مربعند (تقارن مساله) که در طی زمان کوچک میشه و وقتی همزمان بهم می رسند که طول ضلع این مربع صفر بشه.
اما طول مسیر پیموده از شکل 2 بدست میاد. فرض کنید فاصله اولیه a باشه و پس از طی زمان dt حیوانات باندازه dx حرکت کنند. همونطوریکه مشخصه با توجه به کوچک بودن جابجایی، راس بالای ضلع مربع جدید (که با خط قرمز پیوسته نشون داده شده) در جهت عمود بر این ضلع حرکت می کنه و هیچ اثری در تغییر طول نداره. اما راس پایین این ضلع دقیقا در جهت این خط حرکت می کنه. پس تغییر طول ضلع باندازه جابجایی حیوانات هست. از اونجا که شکل مربعی همواره حفظ میشه، این منطق همواره برقراره و پس از طی مسافت a این چهار حیوان بهم میرسند و زمان طی مسیر هم برابره با a/v.
برای اولین بار اقدام به یک مدلسازی درست ریاضی برای مسئله می‌کنند (شکل ۲) . با این مدل برای حل کامل مسئله نیاز به حل یک معادله‌ی دیفرانسیل ساده و انتگرال‌گیری بود که ادامه نداده‌اند. البته ایشان اشکال بسیار واضح جهت فهم راه‌حل گذاشتند که در درک مسئله و همینطور درک کن از درک ایشون بسیار تاثیرگذار هست. متاسفانه ایشون مدلسازی درستشون رو ادامه ندادن و در اداماه با استفاده از تقارن به نحوی به جواب آخر یکی از بخش‌های سوال یعنی زمان رسیدن به همدیگر رسیدن که البته درسته.
راجع به سوالی که داشتن راجع به مسیر (با حداقل یک پارامتر) خب از صورت سوال و همینطور از خود جواب مشخص هست که وقتی شما مسیر رو در ریاضیات تعریف می‌کنید همواره این مسیر پارامتری هست. به خاطر اینکه جناب sabayon بعدا جواب کامل رو گذاشتند و مسیر رو هم ارائه دادند دیگه نیازی به راهنمائی نبود. ازونجائی که من دوستان رو به ارائه‌ی مدلهای مختلف (ولی درست) دعوت کرده بودم خوب تعیین مسیر ممکن بود به شکل‌های پارامتری مختلف باشه اما قطعا اون معادلات با حداقل یک پارامتر که مبین مسیر هست باید ارائه میشد. در این سوال ۳ مدل درست (که البته یکیش شهودی بود) ارائه شد.
بهر صورت اگر ضلع مربع a باشه پس طبق شکل 2 خواهیم داشت: 
و خب طول اولیه‌ی یا شرایط اولیه هم همون a است.
به خاطر اینکه زاویه‌ی 
که زاویه‌ی مقابل ضلع dx هست بسیار کوچیک هست (و سینوس برابر خود قوس کمان هست) اگر از رابطه‌ی بالا انتگرال بگیریم خواهیم داشت:
که همون قضیه‌ی کوچیک شدن مربع رو نشون میده و خب وقتی به هم میرسند که S(t) که تابع فاصله برحسب پارامتر زمان هست صفر شده باشه و بنابراین زمان رسیدن برابر 
است.
حالا بیایم سر مسیر که کمی پیچیده‌تره (فقط کمی) برای پیدا کردن مسیر خب میتونیم از دوران مربع استفاده کنیم دوران مربع هم یعنی زاویه ی آلفا. اگر دیفرانسیل زاویه را بخواهیم به دست بیاریم به راحتی با توجه به دیفرنس بودن میتونیم بنویسیم: 
خب ارتباط S با پارامتر زمان رو که بدست آوردیم پس:
این معادله با نتیجه‌ی قبلی تناسب داره وقتی که زمان a/V طی میشه زاویه‌ی الفا هم به سرعت به سمت بینهایت میره و این یعنی پیچیده شدن سیاه‌چاله‌ای حیونها در هم (البته در عمل حیونا شکل و طول و عرض دارند). این در حالی بود که مدل شهودی پیش‌بینی می‌کرد احتمالا نقاط هیچ‌وقت به هم نمی‌رسند اما ریاضی نشون داد که پس از طی زمانی به هم میرسند. این یادآور پارادوکس زنون هست (
[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]
:ناقص و
[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]
: کامل ).
خب به دست آوردن پاارمتر کل مسیر ازین مدل کمی مشکل هست و به خاطر وقت من ازش صرفنظر میکنم (احتمالا مثل کلکی که فرما زد). هرچند اگر بخواهیم از راه‌حل قطبی که sabayon رفته استفاده کنیم اینجا معادله‌ی چرخش نسبت به زمان رو داریم و تنها کافی هست که معادله‌ی فاصله از مرکز نسبت به زمان رو بدست آوریم. که همون معادله‌ی میشه پس بدون اینکه نیازی به کلک Pierre de Fermat باشه میشه معادله ی مسیر رو به شکل پارامتری اینطور نوشت:
که آلفا زاویه‌ی تعریف شده د شکل (۲) هست و S هم طول ضلع مربع هست اما ازونجائی که این حیونها همیشه ۴ طرف کی مربع هستند پس فاصله تا مرکز هم نصف طول ضلع مربع هست. درسته که این معادله معادله‌ی مبین استانداردی نیست ولی خب درسته و یه راه منطقی این استفاده از مختصات قطبی هست که sabayon استفاده کرده. میشه ازین دو معادله مثلا یک معادله‌ی پارامتری مبتنی بر مختصات کارتزین رو با تبدیلات فراوان به دست آورد که اگر علاقمند بودید به عنوان تمرین روش کار کنید. برای حل متعارف خب راه‌حل sabayon رو می‌تونید نگاه کنید.
جناب Iron، مسئله رو درست مدلسازی کردند. البته منظورم از مشارکت ایشون بحث مارپیچ‌ها و شکل ها نیست که قبلا مطرح شده بود. بلکه بحث استفاده از دیفرنس ضلع و ارتباطش با زمان و سرعت و زاویه هست (شکل ۲). همینطور ایشون برای اولین بار به درستی به زمان (یکی از خواسته‌های مسئله) اشاره کرده بودند. البته برای حل اون از تقارن مسئله عوض حل معادلات دیفرنسی که ایجاد کرده بودند استفاده کردند به همین خاطر ایشون ۳ امتیاز کسب می‌کنند.
و اما جواب جناب sabayon در این
[ برای مشاهده لینک ، با نام کاربری خود وارد شوید یا ثبت نام کنید ]
:
۱. ایشون باز به خوبی از تقارن مسئله جهت ساده‌سازی مسئله استفاده کرده‌اند و به موقعیت‌های حیونها در این سیستم اشاره کردند (البته در مختصات کارتزین) ولی خوب میشه اینرو به معادل قطبیش تبدیل کرد.
۲. راجع به کلیت مسئله ایشون مدلسازی درستی داشتند و راه‌حلشون تقریبا کامل بود. ضمن اینکه نوع استراتژی حل مسئله با استراتژی Iron فرق داشت البته من منتظر مدلهای بیشتر برای حل از طرف دوستان بودم. یک ایراد کار ایشون اینه که با توجه به اینکه سرعت رو V گرفتند (در حالیکه همونطوری که در صورت مسئله اومد می‌تونست فقط تندی بگیره یعنی بدون جهت) اقدام به تجزیه‌ی سرعت روی دو مولفه کردند و خب مسیر حرکت لابد از میان دو مولفه‌ی عمود برهم با زاویه‌ی ۴۵درجه می‌گذره که به این نتیجه رسیدند و خب این فرض سبب یک ضریب ثابت در رابطه‌ها شده و این به خاطر فرض سرعت بودن هست که ما آزاد گذاشتیم پس غلط نیست فقط باعث میشه جواب با مدلهای دیگه کمی متفاوت باشه.
البته ایرادی که من اینجا دارم اینه که ایشون طبق چه استنتاجی زاویه‌ی V رو نسبت به مولفه‌ی شعاعی برابر ۴۵ درجه گرفتند. بهتر بود حداقل به اثر تقارن در این مورد اشاره می‌کردند.
۳. ایشان ابتدا معادله ی مسیر را بدست آورده‌اند و بعد زمان را محاسبه کرده‌اند اما طبق توضیحی که در بند ۲ دادم، اینبار اون مسئله رو به تعبیر خودشون اصلاح کردند و به همون جواب بالا رسیدیند (بدون ضریب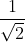 
)
جواب ایشان کامل است، مدلی هم که ارائه دادند مدل درست و مناسبی است. اما بخشی از مشارکت ایشان قبلا انجام شده است. به همین خاطر ایشان ۵ امتیاز را دریافت می‌کنند.
بدین ترتیب امتیازات دوستان:
نوشته شده توسط javid98
محتوای مخفی: محتوای مخفی 
س
