رمزنگاری
رمزنگاری دانش تغییر دادن متن پیام به کمک یک کلید رمزنگاری و یک الگوریتم رمزنگاری است. به صورتی که تنها شخصی که از کلید و الگوریتم مطلع است قادر به استخراج متن اصلی از متن رمزشده باشد و شخصی که از یکی یا هردوی آنها اطلاعی ندارد، نتواند به محتوای پیام دسترسی پیدا کند. رمزنگاری از طریق پنهان نگاه داشتن الگوریتم منسوخ است. در روشهای جدید رمزنگاری فرض بر آن است که همگان الگوریتم را میدانند. آنچه پنهان است فقط کلید است.
رمزنگاری علمی است که به وسیله آن میتوان اطلاعات را بصورتی امن منتقل کرد حتی اگر مسیر انتقال اطلاعات (کانالهای ارتباطی) ناامن باشد. دریافتکننده اطلاعات آنها را از حالت رمز خارج میکند (decrypting). به این عمل در واقع رمزگشایی گفته میشود .
توجه داشته باشید که رمزنگاری به تغییر ساده محتویات یک متن گفته میشود با کدگذاری (coding) تفاوت دارد. در این صورت تنها هر کاراکتر با یک نماد تغییر میکند. کلمه Cryptography بر گرفته لغات یونانی‘kryptos’ به مفهوم ” محرمانه ” و grapheinبه معنای نوشتن ” است. قبل از هر چیز لازم است بین رمز و کد تفاوت قایل شویم. رمز به مفهوم تبدیل کاراکتر به کاراکتر یا بیت به بیت ؛ بدون تغییر محتویات زبان شناختی آن است. در مقابل ” کد ” تبدیلی است که کلمهای را با یک کلمه یا نماد دیگر جایگزین میکند . در بررسی نخستین استفاده کنندگان از رمزنگاری به ” سزار ” امپراتور روم و نیز ” الکندی ” که یک مسلمان است برمیخوریم از عمده ترین شیوههای رمزنگاریهای ابتدایی پیچیدن نسخه اصلی پیام بر روی استوانهای با قطر مشخص و نوشتن پیام بر روی متن استوانهای است. بدیهی است بدون درک میزان قطر، خواندن پیام کار بسیار دشواری بود بعدها از این روش به همراه موتورهای الکتریکی برای رمزنگاری استفاده شد. در ادامه تصاویری از این رمزنگاری را مشاهده میکنید .
رمزنگاری امروزه به طور خاص در علم مخابرات مورد استفاده قرار میگیرد. از رمزنگاری میتوان برای تأمین امنیت و تأمین اعتبار پیام به صورت جداگانه یا توامان استفاده کرد. منظور از تأمین امنیت پیام این است که به غیر از گیرنده مجاز، شخص دیگر قادر به فهمیدن متن پیام نباشد. همچنین منظور از اعتبار پیام این است که فرستنده واقعی پیام مشخص باشد. دانش رمزنگاری بر پایه مقدمات بسیاری از قبیل تیوری اطلاعات، نظریه اعداد و آمار بنا شدهاست.
الگوریتمهای مختلفی (مانند md۵ و RSA) برای رمز کردن اطلاعات وجود دارد.
۱ - معرفی رمزگذاری
رمزگذاری یعنی تبدیل اطلاعات به یک شکل غیر قابل فهم و انتقال آن و سپس برگرداندن اطلاعات رمز شده به حالت اولیه و قابل خواندن. عناصر مهمی که در رمزگذاری مورد استفاده قرار میگیرند به شرح زیر میباشد:
۱.۱ Public Key یا کلید عمومی اعداد یا کلماتی که با یک شخص یا سازمان در ارتباط میباشد. کلید عمومی جزیی از جفت کلید عمومی/خصوصی میباشد وبه صورت عمومی در دسترس کسانی که قصد انتقال اطلاعات رمز شده را دارند، میباشد.
۱.۲ Private Key یا کلید خصوصی اعداد یا کلماتی که با یک شخص یا سازمان در ارتباط میباشد. کلید خصوصی جزیی از جفت کلید عمومی/خصوصی میباشد. کلید خصوصی فقط در دسترس مالک جفت کلید عمومی/خصوصی میباشد و برای بازگشایی اطلاعاتی که توسط کلید عمومی رمزگذاری شده استفاده میشود.
۱.۳ ایجادکنندههای جفت کلید برای ایجاد یک جفت کلید عمومی و خصوصی طبق یک الگوریتم رمزگذاری مشخص استفاده میشود.
۱.۴ Key Factories برای تبدیل کلیدهای نامشخص به کلیدهای مشخص به کار میرود.
۱.۵ Keystores بانکی که برای مدیریت تعدادی از کلیدها به کار میرود.
۱.۶ الگوریتمهای رمزگذاری الگوریتمها و روشهایی که برای رمزگذاری اطلاعات به کار میرود. RSA و DES نام دو تا از معروفترین الگوریتمها میباشد.
۲ - روشهای رمزگذاری
۲.۱ - روش متقارن Symmetric در این روش هر دو طرفی که قصد رد و بدل اطلاعات را دارند از یک کلید مشترک برای رمزگذاری و نیز بازگشایی رمز استفاده میکنند.در این حالت بازگشایی و رمزگذاری اطلاعات دو فرآیند معکوس یکدیگر میباشند. مشکل اصلی این روش این است که کلید مربوط به رمزگذاری باید بین دو طرف به اشتراک گذاشته شود و این سوال پیش میآید که دو طرف چگونه میتوانند این کلید را به طور امن بین یکدیگر رد و بدل کنند. انتقال از طریق انترانت و یا به صورت فیزیکی تا حدی امن میباشد اما در انتقال آن در اینترنت به هیچ وجه درست نیست.در این قبیل سیستمها، کلیدهای رمزنگاری و رمزگشایی یکسان هستند و یا رابطهای بسیار ساده با هم دارند .این سیستمها را سیستمهای متقارن یا ” تک کلیدی ” مینامیم. به دلیل ویژگی ذاتی تقارن کلید رمزنگاری و رمزگشایی، مراقبت و جلوگیری از افشای این سیستمها یا تلاش در جهت امن ساخت آنها لازم است در بر گیرنده ” جلوگیری از استراق سمع ” و ” ممانعت از دستکاری اطلاعات ” باشد .
۲.۲ - روش نامتقارن Asymmetric این روش برای حل مشکل انتقال کلید در روش متقارن ایجاد شد. در این روش به جای یک کلید مشترک از یک جفت کلید به نامهای کلید عمومی و خصوصی استفاده میشود. در این روش از کلید عمومی برای رمزگذاری اطلاعات استفاده میشود. طرفی که قصد انتقال اطلاعات را به صورت رمزگذاری شده دارد اطلاعات را رمزگذاری کرده و برای طرفی که مالک این جفت کلید است استفاده میشود. مالک کلید، کلید خصوصی را پیش خود به صورت محرمانه حفظ میکند. در این دسته، کلیدهای رمزنگاری و رمزگشایی متمایزند و یا اینکه چنان رابطه پیچیدهای بین آنها حکم فرماست که کشف کلید رمزگشایی با در اختیار داشتن کلید رمزنگاری، عملا ناممکن است.
۲.۳ -مقایسه رمزنگاری الگوریتمهای متقارن و الگوریتمهای کلید عمومی: بحثهای زیادی شده که کدام یک از این الگوریتمها بهترند اما جواب مشخصی ندارد. البته بررسی هایی روی این سوال شده به طور مثال Needham و Schroeder بعد از تحقیق به این نتیجه رسیدند که طول پیغامی که با الگوریتمهای متقارن میتواند رمزنگاری شود از الگوریتمهای کلید عمومی کمتر است. و با تحقیق به این نتیجه ریسیدند که الگوریتمهای متقارن الگوریتمهای بهینه تری هستند. اما وقتی که بحث امنیت پیش می آید الگوریتمهای کلید عمومی کارایی بیشتریدارند. و بطور خلاصه میتوان گفت که الگوریتمهای متقارن دارای سرعت بالاتر و الگوریتمهای کلید عمومی دارای امنیت بهتری هستند. در ضمن گاهی از سیستم ترکیبی از هردو الگوریتم استفاده میکنند که به این الگوریتمها الگوریتم های ترکیبی (hybrid)گفته میشود. اما اگر به طور دقیق تر به این دو نگاه کنیم آنگاه متوجه خواهیم شد که الگوریتمهای کلید عمومی و الگوریتمهای کلید متقارن دارای دو ماهیت کاملاً متفاوت هستند و کار بردهای متفاوتی دارند به طور مثال در رمزنگاریهای ساده که حجم دادهها بسیار زیاد است از الگوریتم متقارن استفاده میشود زیرا دادهها با سرعت بالاتری رمزنگاری و رمزگشایی شوند. اما در پروتکل هایی که در اینترنت استفاده میشود، برای رمز نگری کلید هایی که نیاز به مدیریت دارند از الگوریتمهای کلید عمومی استفاده میشود.
۲.۶ – Key Agreement همانطور که در بالا گفته شد به علت کند بودن و محدودیت رمزگذاری با روش نامتقارن از این روش فقط برای رمزگذاری کلید مشترک استفاده میشود. اما این روش نیز یک مشکل دارد و آن اینست که هر شخص نیاز به کلید عمومی و خصوصی مربوط به خود را دارد و باید برای انتقال اطلاعات آن را برای طرف مقابل بفرستد. یک راه برای حل مشکل استفاده از کلید عمومی و یک مکانیزم به نام Key Agreement میباشد که به طبق آن یک توافق بر روی کلید مخفی بین طرفین به وجود میآید و به این ترتیب نیازی به انتقال کلید نیست. وقتی که یک بار بر روی یک کلید مشترک توافق حاصل شد از آن میتوان برای رمزگذاری و رمزگشایی اطلاعات مربوطه استفاده کرد. معمولاً در این روش از الگوریتم Diffie-Hellman استفاده میشود. مراحل انتقال اطلاعات از این روش به صورت زیر میباشد: - آغازگر ابتدا یک جفت کلید عمومی و خصوصی ایجاد کرده و کلید عمومی را همراه با مشخصات الگوریتم (Algorithm Specification) به سمت طرف مقابل میفرستد. - طرف مقابل نیز یک جفت کلید عمومی و خصوصی همراه با مشخصات الگوریتم آغازگر ساخته و کلید عمومی را برای آغازگر میفرستد. - آغازگر یک کلید مخفی بر اساس کلید خصوصی خود و کلید عمومی طرف مقابل ایجاد میکند. - طرف مقابل نیز با استفاده از کلید خصوصی خود و کلید عمومی آغازگر یک کلید مخفی میسازد. الگوریتم Diffie-Hellman تضمین میکند که کلید مخفی هر دو طرف یکسان میباشد.
۳ - انواع روشهای رمزگذاری اسناد
۳.۱ - رمزگذاری همه اطلاعات یک سند xml سند زیر را در نظر بگیرید:
<?xml version=’۱.۰′?> <PaymentInfo xmlns=’http://example.org/paymentv۲′>
<Name>John Smith</Name>
<CreditCard Limit=’۵,۰۰۰′ Currency=’USD’>
<Number>۴۰۱۹ ۲۴۴۵ ۰۲۷۷ ۵۵۶۷</Number>
<Issuer>Example Bank</Issuer> <Expiration>۰۴/۰۲</Expiration> </CreditCard> </PaymentInfo>
این سند پس از رمزگذاری بر اساس استانداردهای W۳C به شکل زیر در میآید:
<?xml version=’۱.۰′?> <EncryptedData xmlns=’
کد:
برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید
MimeType=’text/xml’>
<CipherData>
<CipherValue>A۲۳B۴۵C۵۶</CipherValue>
</CipherData>
</EncryptedData>
رمزگذاری یک element مشخص بصورت زیر میباشد. در این حالت <CreaditCard> رمزگذاری شده و به شکل زیر در آمدهاست:
<?xml version=’۱.۰′?> <PaymentInfo xmlns=’http://example.org/paymentv۲′>
<Name>John Smith</Name>
<EncryptedData Type=’
کد:
برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید
xmlns=’http://www.w۳.org/۲۰۰۱/۰۴/xmlenc#’>
<CipherData>
<CipherValue>A۲۳B۴۵C۵۶</CipherValue>
</CipherData>
</EncryptedData>
</PaymentInfo>
<?xml version=’۱.۰′?>
<PaymentInfo xmlns=’http://example.org/paymentv۲′>
<Name>John Smith</Name>
<CreditCard Limit=’۵,۰۰۰′ Currency=’USD’>
<EncryptedData xmlns=’
کد:
برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید
Type=’http://www.w۳.org/۲۰۰۱/۰۴/xmlenc#Content’>
<CipherData>
<CipherValue>A۲۳B۴۵C۵۶</CipherValue>
</CipherData>
</EncryptedData>
</CreditCard>
</PaymentInfo>
اطلاعات پس از رمزگذاری طبق استاندارد W۳C درون عنصر <ChipherData> قرار میگیرند. همچنین در این قسمت یک عنصر <EncryptedData> دیده میشود که شامل اطلاعاتی از قبیل نوع رمزگذاری و یا الگوریتم مورد استفاده برای رمزگذاری میباشد.
۳.۴ – کلیدهای مورد استفاده در رمزگذاری وقتی یک سند XML یا بخشی از آن رمزگذاری میشود آن قسمت با عنصر <EncryptedData> تعویض میشود. این عنصر ممکن است شامل نوع رمزگذاری باشد که گیرنده از این اطلاعات استفاده میکند، مثلاً اطلاعاتی شامل اینکه آیا کل سند رمزگذاری شده یا قسمتی از آن و همچنین اینکه نوع اطلاعات رمزگذاری شده متن است یا تصویر و غیره.
میتوان مشخصات کلید مشترک را درون خود سند درون عنصر <EncryptedKey> قرار داد. اطلاعات واقعی که رمزگذاری شدهاند درون عنصر <CipherData> قرار میگیرند. در داخل این قسمت نیز یک عنصر <CipherValue> قرار دارد که شامل اطلاعات واقعی رمزگذاری شده میباشد.
۳.۵ – روشهای انتقال کلید طبق استاندارد W۳C سه روش برای انتقال کلید موجود میباشد:
۱. میتوان کلید را درون همان سند قرار داد، عناصر <EncryptedData> و یا <EncryptedKey> میتوانند یک عنصر <ds:KeyInfo> داشته باشند که مشخص کننده جزییات کلید میباشد. خود این عنصر شامل عناصر زیر میباشد: - عنصر <ds:KeyValue> که مقدار آن همان کلید عمومی یا کلید رمزگذاری شده میباشد. - عنصر <ds:KeyName> که به یک عنصر <EncryptedKey> اشاره میکند. - عنصر <ds:RetrievalMethod> که متد بازیابی کلید را مشخص میکند.
۲. میتوان یک فایل دیگر که شامل عنصر <EncryptedKey> میباشد ضمیمه سند کرد که در این حالت درون سند xml عنصر <DataReference> یا <KeyReference> قرار میگیرد که به آن ضمیمه اشاره میکند. ۳. در روش سوم در هیچ قسمت از سند XML به کلید اشارهای نمیشود و مسیر کلید از قبل مشخص میباشد.
۴ – امضای دیجیتالی ۴.۱ – معرفی امضای دیجیتالی برای اینکه هویت فرستنده سند تایید شود و نیز برای اطمینان از اینکه سند در طول مدت انتقال به گیرنده دستکاری نشدهاست از امضای دیجیتالی استفاده میشود. میتوان کل یک سند و یا قسمتی از آن را امضا کرد. به طور کلی سه دلیل برای استفاده از امضای دیجیتالی وجود دارد که شامل: ۱. استفاده از کلید عمومی این اجازه را به هر شخصی میدهد که کلید خود را به سمت فرستنده اطلاعات بفرستد و سپس گیرنده پس از دریافت اطلاعات آن را توسط کلید خصوصی خود بازگشایی میکند، بنابراین امضای دیجیتالی این امکان را میدهد که فرستنده یا گیرنده مطمین شوند که اطلاعات از محل یا شخص مورد نظر دریافت میشود. ۲. اطلاعات در طول مدت انتقال ممکن است توسط دیگران دستکاری شود برای اینکه از صحت اطلاعات رسیده مطمین شویم نیاز به یک امضای دیجیتالی در این حالت احساس میشود. ۳. رد کردن اطلاعات فرستاده شده. گیرنده اطلاعات برای اینکه مطمین شود فرستنده بعدا از اطلاعاتی که فرستاده اعلام بی خبری نکند و آنها را رد نکند از فرستنده یک امضا درخواست میکند تا شاهدی بر این ادعا باشد.
برای پیاده سازی یک امضای دیجیتالی نیاز به سه الگورتم داریم: - یک الگوریتم برای ایجاد کلید - الگوریتم برای ایجاد امضا - الگوریتم برای تایید امضا
برای ایجاد یک امضای دیجیتالی باید یک عدد checksum برای سند مورد نظر محاسبه شود. فرض کنید Bob قصد ارسال یک پیام به Alice را دارد، Bob پیام خود را همراه با امضای دیجیتالی برای Alice میفرستد. این امضای دیجیتالی توسط کلید خصوصی که مالک آن Bob میباشد ایجاد شدهاست. در سمت دیگر Alice با استفاده از الگوریتم تایید امضا و کلید عمومی که از Bob دریافت کرده صحت امضا و اینکه امضا از طرف Bob میباشد را تایید میکند.
۴.۲ – عناصر موجود در یک امضا در شکل زیر عناصر تشکیل دهنده یک امضای دیجیتالی را میبینید:
برای ایجاد یک امضای دیجیتالی باید طبق استاندارد W۳C به صورت زیر عمل کرد:
۱. ابتدا باید منبعی را که قصد امضای آن را دارید مشخص کنید. عنصر <Reference> که در شکل دیده میشود مشخص میکند که چه چیزی در این قسمت امضا و علامت گذاری شدهاست. این منبع به صورت یک آدرس URI میباشد:
کد:
برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید
به یک منبع از نوع فایل HTML اشاره میکند.
کد:
برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید
به یک فایل تصویری اشاره میکند.
کد:
برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید
به یک فایل از نوع XML اشاره میکند.
کد:
برای مشاهده محتوا ، لطفا وارد شوید یا ثبت نام کنید
به یک عنصر درون فایل XML به نام main اشاره میکند.
۱. testInfo: به یک عنصر درون فایل XML فعلی اشاره میکند.
۲. محاسبه مقدار digest به ازای هر منبع مشخص شده در <Reference>، که این مقدار در <DigestValue> قرار میگیرد. همچنین عنصر <Reference> شامل عنصر <DigestMethod> میباشد که الگوریتم مورد استفاده در محاسبه digest را معرفی میکند.
۳. همه منابع که باید امضا شوند جمع آوری میشود:
SignedInfo Id="foobar">
<CanonicalizationMethod
Algorithm="http://www.w۳.org/TR/۲۰۰۱/REC-xml-c۱۴n-۲۰۰۱۰۳۱۵"/>
<SignatureMethod Algorithm="http://www.w۳.org/۲۰۰۰/۰۹/xmldsig#dsa-sha۱" />
<Reference URI="http://www.abccompany.com/news/۲۰۰۰/۰۳_۲۷_۰۰.htm">
<DigestMethod Algorithm="http://www.w۳.org/۲۰۰۰/۰۹/xmldsig#sha۱" />
<DigestValue>j۶lwx۳rvEPO۰vKtMup۴NbeVu۸nk=</DigestValue>
</Reference>
<Reference
URI="http://www.w۳.org/TR/۲۰۰۰/WD-xmldsig-core-۲۰۰۰۰۲۲۸/signature-example.xml">
<DigestMethod Algorithm="http://www.w۳.org/۲۰۰۰/۰۹/xmldsig#sha۱"/>
<DigestValue>UrXLDLBIta۶skoV۵/A۸Q۳۸GEw۴۴=</DigestValue>
</Reference>
</SignedInfo>
عنصر <CanonicalizationMethod> مشخص میکند که چه الگوریتمی برای قانونی کردن (canonize) عنصر <SignedInfo> استفاده شدهاست.
۴. علامت گذاری امضا: در این قسمت مقدار digest برای عنصر <SignedInfo> محاسبه شده و درون عنصر <SignatureValue> قرار میگیرد. ۵. اضافه کردن مشخصات کلید: میتوانید مشخصات کلید خود را درون عنصر <KeyInfo> قرار دهید ولی این قسمت الزامی نیست و ممکن است شما نخواهید که این مشخصات معلوم گردد.
۴.۳ – تایید یک امضای دیجیتالی مراحل تایید Verify یک امضای دیجیتالی به صورت خلاصی در زیر آورده شدهاست: - تایید امضای عنصر <SignedInfo>. برای این منظور ابتدا دوباره مقدار digest برای این عنصر را طبق الگوریتم مشخص شده در عنصر <SignatureMethod> محاسبه نموده و از کلید عمومی برای این کار استفاده میشود و برای تایید آن مقدار محاسبه شده را با مقدار معرفی شده در عنصر <SignatureValue> مقایسه میکنیم. - اگر مرحله قبل بدون مشکل تایید شد حالا به ازای هر منبع معرفی شده در عنصر <Reference> مقدار digest آن را محاسبه نموده و با مقدار مشخص شده در عنصر <DigestValue> مقایسه میکنیم.





 جواب بصورت نقل قول
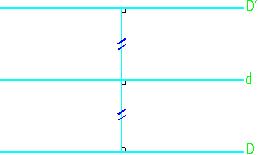
جواب بصورت نقل قول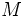 نسبت به خط
نسبت به خط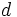 نقطه
نقطه است در صورتی که، خط
است در صورتی که، خط باشد .
باشد . نشان می دهیم .هر نقطه که روی خط
نشان می دهیم .هر نقطه که روی خط
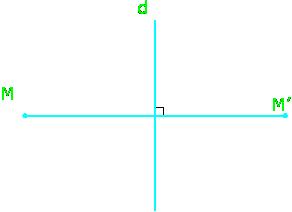
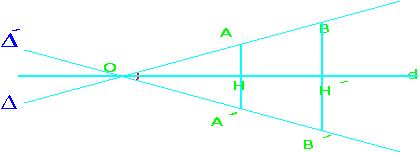
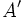 قرینه
قرینه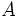 نسبت به
نسبت به با خط
با خط قرینه خط
قرینه خط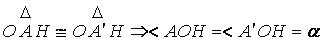
 نقطه ی دلخواهی از خط
نقطه ی دلخواهی از خط قطع کند، از تساوی دو مثلث
قطع کند، از تساوی دو مثلث و
و ( ز-ض-ز) نتیجه می شود که :
( ز-ض-ز) نتیجه می شود که :
 ، پس قرینه ی هر نقطه دلخواه خط
، پس قرینه ی هر نقطه دلخواه خط
 ، بنابراین :
، بنابراین :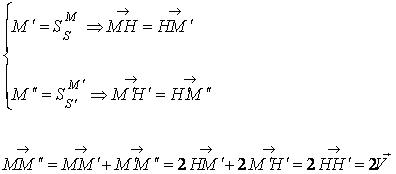
 یا
یا 



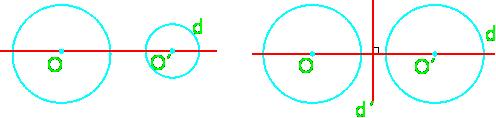
 آنگاه زاویه ی دوران ۱۸۰ است یعنی نتیجه ترکیب دو تقارن محوری با محورهای عمود بر هم یک تقارن مرکز است .
آنگاه زاویه ی دوران ۱۸۰ است یعنی نتیجه ترکیب دو تقارن محوری با محورهای عمود بر هم یک تقارن مرکز است .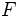 نسبت به خط ثابت
نسبت به خط ثابت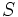 بر روی خود شکل قرار گیرد خط
بر روی خود شکل قرار گیرد خط  ضلعی منتظم دارای
ضلعی منتظم دارای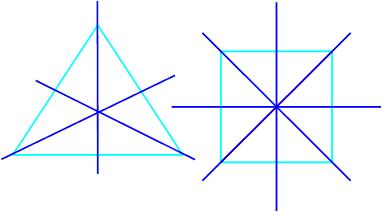
 باشد، که ارتفاع آن
باشد، که ارتفاع آن است ، حال اگر قاعده مشترک را
است ، حال اگر قاعده مشترک را پس ارتفاع ثابت است و مکان هندسی راس
پس ارتفاع ثابت است و مکان هندسی راس می باشد .
می باشد . مینیمم باشد (
مینیمم باشد (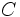 را نسبت به خط
را نسبت به خط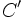 می نامیم . از
می نامیم . از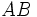 و
و مساوی و مثلث
مساوی و مثلث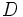 روی ضلع
روی ضلع 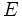 و
و  کمترین مقدار ممکن را داشته باشد .
کمترین مقدار ممکن را داشته باشد .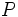 و
و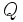 قرینه های
قرینه های ،
، . پس محیط مثلث
. پس محیط مثلث نقاط دیگری روی
نقاط دیگری روی باشند محیط مثلث
باشند محیط مثلث  برابر طول پاره خط شکسته
برابر طول پاره خط شکسته است که به وضوح از طول پاره خط
است که به وضوح از طول پاره خط
 یکی از مربع های مذکور باشد و
یکی از مربع های مذکور باشد و  یکی از محورهای تقارن و
یکی از محورهای تقارن و قرینه ی
قرینه ی 
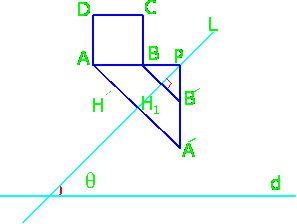
 ( مطابق شکل ) . حال از آنجا که
( مطابق شکل ) . حال از آنجا که
 . پس چهار نوع تقارن داریم ، که در شکل شماره گذاری شده اند :
. پس چهار نوع تقارن داریم ، که در شکل شماره گذاری شده اند :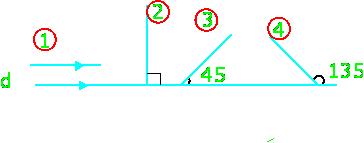
 مبدا مختصات باشد و
مبدا مختصات باشد و  مرکز یکی از مربع ها باشد . (واضح است که با توجه به یکسان بودن مربع ها و مختصات مرکز آنها و مربع ها به طور یکتا تعیین می شوند)
مرکز یکی از مربع ها باشد . (واضح است که با توجه به یکسان بودن مربع ها و مختصات مرکز آنها و مربع ها به طور یکتا تعیین می شوند)
 موجود باشد آنگاه
موجود باشد آنگاه موجود است پس خط
موجود است پس خط نیز یک محور تقارن است و شکل حاصل ۳ محور تقارن دارد .
نیز یک محور تقارن است و شکل حاصل ۳ محور تقارن دارد . و
و آنگاه از هر مربع
آنگاه از هر مربع  مربع ( با خود مربع) حاصل می شود .
مربع ( با خود مربع) حاصل می شود . و
و آنگاه از هر مربع
آنگاه از هر مربع  مربع ( با خود مربع) حاصل می شود .
مربع ( با خود مربع) حاصل می شود . و
و آنگاه از هر مربع
آنگاه از هر مربع  مربع ( با خود مربع) حاصل می شود .
مربع ( با خود مربع) حاصل می شود . و
و آنگاه از هر مربع
آنگاه از هر مربع  آنگاه از هر مربع یک و فقط یک مربع ( یعنی خود مربع ) حاصل می شود . از حالات فوق نتیجه می شود که تعداد مربع ها به شکل
آنگاه از هر مربع یک و فقط یک مربع ( یعنی خود مربع ) حاصل می شود . از حالات فوق نتیجه می شود که تعداد مربع ها به شکل و
و می باشد .
می باشد .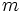 به معادله ی
به معادله ی و دیگری
و دیگری به معادله
به معادله باشد و
باشد و مرکز یکی از مربع ها باشد
مرکز یکی از مربع ها باشد 

 بی نهایت نقطه به شکل
بی نهایت نقطه به شکل داریم : پس بی نهایت مربع داریم ( تناقض).
داریم : پس بی نهایت مربع داریم ( تناقض).


.gif)

