دکارت
می اندیشم پس هستم - مروری بر دکارت و فلسفه او
رنه دکارت علاوه بر فیلسوف از ریاضیدانان و فیزیکدانان بزرگ عصر رنسانس نیز بوده است، طوریکه او را پدر هندسه تحلیلی نیز نامیده اند. او در ۳۱ مارس ۱۵۹۶ در فرانسه به دنیا آمد و پس از طی دوره تحصیلی هشت ساله در بیست سالگی به جهان گردی پرداخت و از آن پس به قول خودش کوشید در پی خرد برود. از این رو به ارتش هلند پیوست و به جنگ رفت و بدین ترتیب اوقاتی از عمر را در قسمتهای گوناگون اروپا گذراند در ۱۶۲۹ باز هم روانه هلند شد و نزدیک بیست سال در آنجا و در آرامش به تحقیقات خود پرداخت. تحقیقات دکارت بیشتر تجربه و تفکر شخصی بود، او کمتر از کتاب و نوشته استفاده می کرد و این ما را یاد سقراط می اندازد که در کوچه های آتن قدم می زد و با هر کس به بحث و فلسفه می پرداخت و هیچ گاه چیزی از خود ننوشت!
دکارت در سپتامبر ۱۶۴۹ به دعوت ملکه سوید برای تعلیم فلسفه خویش به دربار وی در استکهلم رفت اما شرایط آب و هوا و همینطور نوع زندگی که دکارت به آن عادت نداشت او را به بیماری ذات الریه مبتلا ساخت و در ۱۱ فوریه ۱۶۵۰ در همان جا در گذشت.عصری که دکارت در آن می زیست به عصر شکاکیت نیز معروف می باشد و نمایان است که “شک” نه تنها اعتقادات دینی را متزلزل می کند بلکه آسایش و آرامش زندگی را نیز مختل می کند. دکارت نیز که به دیانت مسیحی معتقد و به گفته خودش وجود خداوند را همچون قضایای ریاضی بدیهی می دانست برای بر انداختن شکاکیت و رهانیدن اعتقادات و علوم از چنگال شک به تاسیس فلسفه جدیدی پرداخت، بمین خاطر او را پدر فلسفه نو نیز نامیده اند.
او همانند ارشمیدس که معتقد بود: “برای اینکه بتواند کره خاکی را از جا بر کند و به مکان دیگر منتقل کند تنها نیازمند یک نقطه ثابت و ساکن بود”، به دنبال نقطه ای ثابت می گشت تا بر آن تکیه کند. از اینرو دکارت می گوید: “در ابتدا باید به همه چیز شک کرد” او نمی خواست قدم اول و پایه بنا را بر جای سست قرار دهد. و در ادامه این شک او از این هم فراتر می رود و می گوید: “حتی به حواسمان نیز نمی توانیم اعتماد کنیم، حواسمان ممکن است ما را بفریبند.” اما در این میان تنها چیزی که برای او مسلم بود همین شک کردن او بود. این شک تنها چیزی بود که او یقین داشت و وقتی شک می کند، حتما می اندیشد و چون می اندیشد حتما موجودی اندیشنده است! و یا به گفته خود او: “می اندیشم، پس هستم”. او می گوید: وقتی من حکم می کنم که شییی هست یا موجود است چرا که آنها را می بینم، قطعا با بداهت بیشتری لازم می آید که خود من که شی را میبینم، وجود داشته باشم چون ممکن است آنچه من می بینم در واقع آن شی نباشد، همچنان که ممکن است من حتی چشمی نداشته باشم که چیزی را ببیند ولی محال است وقتی می بینم یا فکر می کنم که می بینم (فرقی نمی کند) خود من که فکر می کنم معدوم باشم.”
او این نقطه ثابت را بدست آورده بود و در ادامه از این نقطه پیش تر می رود و به اثبات و جود خداوند، تجرد نفس، بیان ماهیت خطا، بیان ماهیت ماده و به اثبات عالم خارج می پردازد، که اینها همه در رساله تاملات او جمع آوری شده است.
تاملات نه تنها بهترین اثر دکارت بلکه بهترین و مهمترین اثر قرن هفدهم به شمار آورد.
وجود خدا در نظر دکارت همانند ” هر که اندیشید پس هست” خود - بدیهی بود. او می گفت: تصور وجود کامل را همه ما داریم و لازمه چنین تصوری آن است که باید وجود کاملی وجود داشته باشد چون وجود کامل اگر وجود نمی داشت کامل نمی بود، در ضمن اگر وجود کاملی در میان نبود تصور آن نیز به ذهنمان راه نمی یافت! به گفته دکارت تصور خدا در ذات ماست. این تصور از وقتی که بدنیا می آییم و مثل علامتی که سازنده روی فرآورده خود می گذارد بر ما نقش شده است. چرا که تصور کمال از انسان بی کمال ممکن نیست
جواب بصورت نقل قول
را 
می‌نامیم. در این صورت 
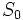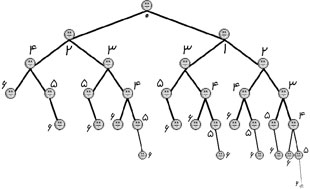
برابر ۱، و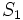 
برابر ۲ است. با اندکی توجه میتوان رابطه‌ای بازگشتی برای این دنباله به دست آورد؛ دو مشتری‌ای که توسط نفر اول وارد بازی شده‌اند یکی یک مرحله و دیگری دو مرحله از رأس اولی عقب‌ترند، و لذا درختی که در مرحله n ام زیر آن دو تشکیل میشود دقیقاً مشابه درخت اصلی در یک مرحله پیش و درخت اصلی در دو مرحله پیش است. نتیجه این که در مرحله n ام در بازوی راست رأس بالایی 
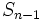نفر و در بازوی چپ 
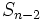نفر قرار دارد. اگر رأس بالایی را هم در نظر بگیریم رابطه بازگشتی زیر به دست می‌آید.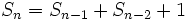
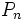بنامیم، به رابطه زیر می‌رسیم:
