مقالات علمي رياضي

[sajadhoosein]

لگاریتم و کاربردهای آن در زندگی





نظریه ها و قاعده های ریاضی، با کشف خود «هستی» پیدا می کنند، آن ها تنها وجود دارند و اغلب بدون کاربردند. دیر یا زود، و گاهی بعد از صدها و هزارها سال، این موجودات ریاضی به «صفت» تبدیل می شوند و کاربرد خود را در زندگی و عمل، در سایر دانش ها، در صنعت و هنر پیدا می کنند.«اویلر» ¼br> ¼br> شاید ۳۸۰ سال پیش کسی فکر نمی کرد لگاریتمی که در رابطه با نیاز محاسبات عملی کشف شد در آینده کاربردهای وسیعی پیدا کند.
شاید هیچوقت کپلر فکر نمی کرد که جدول هایی را که برای ساده کردن محاسبات طولانی در تعیین مدار مریخ و یا کارهای اخترشناسی دیگرش تنظیم کرد، جرقه ای این چنین را در ریاضیات ایجاد کند.
یا شاید لاپلاسی که گفت: “لگاریتم طول زندگی اخترشناسان را چند برابر کرد” نمی دانست که نه تنها طول زندگی اخترشناسان بلکه دریانوردان، بازرگانان، موسیقیدانان، شیمیدانان، ریاضیدانان، زمین شناسان و حتی همه ی انسان های کره ی زمین را چند برابر کرد.
بدیهی است که تا نیاز به چیزی احساس نشود آن چیز کشف و اختراع نمی گردد، در واقع هرکدام از علومی که با آن روبه رو هستیم هریک به مقتضای نیازی و با توجه به هدف خاصی پیکر بندی شده اند.
لگاریتم نیز با توجه به محاسبه های طولانی و ملال آوری که دانشمندان سده های شانزدهم و هفدهم میلادی با آن سر و کار داشتند، بوجود آمد. این محاسبه ها وقت و نیروی زیادی را از دانشمندان تلف می کرد و همیشه دانشمندان در ذهن داشتند که چطور می شود بدون انجام چنین محاسبات پیچیده و دشواری و آن هم در کمترین زمان ممکن به جواب مطلوب دست یابند. گفته می شود که حتی در قرن هشتم هندی ها با محاسبات مربوط به لگاریتم آشنایی داشتند اما این کلمه و مفهوم مربوط می شود به قرن شانزدهم .جدول هایی نیز در این زمینه بوجود آمد و شاید همین تلاش ها و نیازها بود که سر انجام به کشف لگاریتم انجامید تا آن جا که دو دانشمند به طور همزمان و بدون اینکه از کار یکدیگر آگاه باشند موفق به کسب چنین افتخاری گشتند اولی جان نپر و دیگری بورگی.
اما اصطلاح لگاریتم نشات گرفته از فعالیت های نپر است که از واژه ی یونانی «لوگوس» به معنی نسبت و «ارتیوس» به معنی عدد گرفته شده است. او همچنین بجای لگاریتم از اصطلاح عدد ساختگی نیز استفاده می کرد. نپر چکیده ی کارهای خود را در کتابی با عنوان «شرح جدول های عجیب لگاریتمی» چاپ کرد و به دنیا نمایاند.
عدد e (مبنای لگاریتم طبیعی) نیز در چنین سال هایی چشم به جهان و جهانیان گشود. گفته می شود کاشف عددe آن گونه که برخی می پندارنداویلر نبوده است بلکه خود نپر بحث مربوط به لگاریتم طبیعی و عدد e را در یکی از نوشته هایش پیش کشیده است.
بعد از آشکار شدن لگاریتم به جهانیان ابزارهایی برای آسانتر کردن محاسبات لگاریتمی کشف شد که از آن جمله می توان به خط کش لگاریتمی ساخته ی گونتر انگلیسی اشاره نمود. امروزه نیز با استفاده از ماشین حساب و با فشردن یک کلید میتوان عمل لگاریتم گرفتن را به آسانی و سرعت انجام داد.
با ورود لگاریتم به دنیای ریاضیات و آشنا شدن مردم و دانشمندان با آن، این شاخه کاربردهای زیادی را در زندگی روزمره پیدا کرد. چنانکه امروزه لگاریتم در حسابداری و در تعیین بهره ی مرکب و نیز مسائل مالی کاربرد فراوانی یافته است. همان زمان که لگاریتم اختراع شده بود اویلر رابطه ی بین عدد e و بهره ی مرکب را دریافت و فهمید که حد بهره به سمت عددی متناسب (یا مساوی در شرایط خاص) ، که همان عدد e است میل می کند. همچنین از لگاریتم در مدلسازی و بازار یابی سهمی استفاده می شود. مدلسازی ایجاد الگو و تمثیلی برای تجسم واقعیت های خارجی است که در مسائل مربوط به ریاضیات و حسابداری کاربرد دارد.

---------- Post added at 01:28 PM ---------- Previous post was at 01:27 PM ----------

درادامه ی مبحث کاربردهای لگاریتم شاید جالب باشد که بدانیم لگاریتم درهنرنیزکاربرد پیدا می کند. میدانیم درموسیقی برای بیان فشارصوت از دسیبل(Decibel ) استفاده می شود. اصطلاح دسیبل که در بسیاری از مباحث فیزیک موسیقی و نیز به هنگام استفاده از اعمال ضبط و افکت در استودیوهای موسیقی کاربرد دارد در واقع از یک محاسبه ی لگاریتمی فوق العاده آسان قابل محاسبه است.
اصطلاح دسیبل برای مقایسه ی نسبت بین دو مقدار در علوم فیزیک، الکترونیک و بسیاری از رشته های مهندسی استفاده می شود. گفتیم دسیبل در فیزیک صوت کاربرد زیادی دارد، یکی از دلایل استفاده از لگاریتم در این شاخه این است که از آن جایی که هر دو مقداری که قرار است با هم مقایسه شوند دارای ابعاد فیزیکی یا دیمانسیون(Dimention) یکسان هسنتد خارج قسمت آن ها عدد خالص و بدون واحد است، لذا می توان از خارج قسمت آن ها لگاریتم گرفت تا بتوان ساده تر مقادیر بسیار کوچک یا بسیار بزرگ را با هم مقایسه کرد، بدون این که از رقم ها و عددهای بزرگ و کوچک استفاده شود.
بعبارتی دیگر می توان گفت دسیبل واحدی است برای تغییر حجم صدا. البته قبلا برای این کار از واحد بل(مخترع تلفن) استفاده می شد.
کاربردهای لگاریتم در موسیقی در این جا پایان نمی یابد. مثلا لگاریتم در بیان سطح فشار صوت (Sound pressure level) کاربرد می یابد که در آن از معیاری به نام SPL یا سطح فشار صوت استفاده می شود.
همچنین، ساوار موسیقیدان و فیزیکدان فرانسوی که واحد سنجش فواصل موسیقی به نام اوست با استفاده از یکی از خاصیت های لگاریتم(لگاریتم حاصلضرب برابرست با حاصل جمع لگاریتم ها) توانست فواصل موسیقی را با هم جمع یا تفریق کند. بعدها برای اینکه جمع و تفریق آن ها از حالت اعشاری خارج شود واحد «سناوار» را مرسوم کردند.
از مهمترین کاربردهای لگاریتم میتوان به کاربرد آن در علم زلزله شناسی اشاره نمود. مشکلات زیادی در اندازه گیری بیشینه ی دامنه وجود داشت که به توصیه ی گوتنبرگ دانشمند برجسته ی زمین لرزه شناسی اندازه گیری آن بصورت لگاریتم اعشاری انجام شد، امروزه در رابطه ی مقیاس بندی ریشتر و محاسبه ی بزرگی زلزله به لگاریتم بر می خوریم. سال ها بعد چارلز ریشتر زلزله شناس آمریکایی یک مقیاس لگاریتمی را برای سنجش زلزله تعیین کرد که هنوز هم مورد استفاده است و به نام خودش(ریشتر) معروف است. زلزله شناسان نیز انرژی آزاد شده بوسیله ی زلزله، دامنه و فاصله ی زلزله (کانون زلزله) را با محاسبات لگاریتمی اندازه گیری می کنند. البته بزرگی زلزله یک درجه ی قرار داری است اما می توان از طریق آن و بطور نسبی زمین لرزه ها را با یکدیگر مقایسه نمود.
اما باید گفت پرکاربرد ترین علمی که از لگاریتم در آن استفاده می شود شیمی تجزیه است. در شیمی تجزیه بارها و بارها با لگاریتم و عمل لگاریتم گیری مواجه می شویم از آن جمله می توان به استفاده از لگاریتم در اندازه گیری PH ، توابعP ،معادله ی دبای-هوکل که با استفاده از آن می توان ضرایب فعالیت یون ها را از طریق بار و میانگین اندازه ی آن ها محاسبه کرد اشاره نمود.
کاربردهای لگاریتم تنها به موارد اشاره شده در این مقاله ختم نمی شود چنانچه لگاریتم در علوم زیستی، نجوم و در اخترشناسی جهت اندازه گیری فاصله بین ستارگان و سیاره ها، آمار، علوم کامپیوتر، زمین شناسی و… نیز کاربرد می یابد ، چه بسا کاربردهای دیگری را که در آینده از لگاریتم شاهد خواهیم بود.

[sajadhoosein]

آیا صفر یعنی هیچ؟



آرام در کنار آنها نشستم و با علامت دست خواهش کردم بحث خود را ادامه دهند. سه نفر بودند ؛ توکا ، کبوتر و آرش … کبوتر با هیجان و اندکی خشم گفت: - هر چیزی را که نمی شود معنا کرد؛ “بالا” یعنی بالا و “پایین” یعنی پایین. بعد سرش را به طرف توکا برگرداند و گفت: - سرت را بالا بگیر . توکا از روی صندلی بلندشد، ایستاد و سرش را به طرف آسمان گرفت. – حالا ، آرش ، تو سرت را پایین بگیر. آرش بلند شد، کف دو دستش را روی زمین گذاشت و با حرکتی تند، تلاش کرد پاهایش را به طرف آسمان ببرد و روی دو دست خود بایستد ( مثل کسانی که آکروبات می کنند) ولی نتوانست و از سمت دیگر افتاد و پشتش محکم به زمین خورد. فریادی کشید و گفت: - چه کار سختی ؟ من نمی توانم . ولی کبوتر خشمگین تر به او گفت: - چرا خودت را به سادگی می زنی؟ همان جور که روی دو پایت ایستاده ای ، می توانی سرت را “بالا” بگیری؛ به طرف آسمان .( و ادامه داد) می بینید، “بالا” یعنی به طرف آسمان و طرف ستارگان و “پایین” یعنی به طرف زمین . این را همه می فهمند.

آرش زمزمه کرد: - ولی آسمان و ستارگان ، فقط “بالا” نیستند؛ حتی در “پایین” هم ، آسمان و ستاره است. پس به نظر تو “بالا” یعنی جایی که می تواند”پایین” یا “سمت راست” یا “سمت چپ” یا “روبه رو” و “پشت سرهم” باشد؟ توکا دخالت کرد: - “پایین” جایی است که همه چیز به طرف آن می افتد. کبوتر پذیرفت . ولی توکا ادامه داد: - پس آن طور که خیال می کنیم، نمی توان گفت :”بالا” یعنی بالا و “پایین” یعنی پایین . هر چیزی نیاز به تعریف دارد. ولی آرش موضوع را پیچیده تر کرد: - این درست! ما در ایران که در نیمکره شمالی هستیم، با آنها که از جمله در استرالیا ، یعنی نیمکره جنوبی هستند، در دو جهت مختلف ایستاده ایم ؛ “پایین” برای ما و برای آنها در دو جهت مخالف است. نمونه دیگری بیاوریم که در گفت و گوهای معمولی واژه های”بالا” و “پایین” معناهای دیگری هم دارند:”بالاتر از چهار راه” ، “پایین تر از فلان خیابان”.
این جا دیگر “بالا” و “پایین” به آن مفهومی که گفتیم، معنا نمی دهند . در ضمن ، اگر به کسی نشانی منزل خود را این طور بدهید:”پایین تر از چهارراه a و بالاتر از مغازه b ” ، در واقع او را سرگردان کرده اید. چهار خیابان یا کوچه در چهار راه a به هم می رسند؛ کدام طرف را بالا و کدام طرف را بالا و کدام طرف را پایین می دانید؟ … به هر حال ، برای درک آن در نظر گرفت . توکا گفت: من حرف دیگری دارم. – وقتی در هوای سرد زمستان ، نفس خود را بیرون می دهید، بخار آبی که از دهان شما خارج می شود، به طرف زمین نمی رود. وقتی کتری یا سماور می جوشد، باز هم بخار آب در جهت عکس می رود و به زمین نمی رسد. درست است که من گفتم :”پایین جایی است که همه چیز به طرف آن می افتد”؛ ولی مگر بخار آب جزو “همه چیز ” نیست؟ این مشکل را چگونه حل کنیم؟ کبوتر می اندیشید … بعد سرش را بالا گرفت و گفت: - مشکل دیگری هم هست .

من در یک فیلم که به یک سفینه واقعی فضایی مربوط بود، دیدم چیزی به طرف کف فضا پیما نمی افتد، همه چیز در هوا معلق می شود. نمی دانم در این باره چه بگویم؟ در آن “بالا” کجاست و “پایین” کجا؟ آرش دخالت کرد: - آن نقطه “صفر” است، مرز پایین و بالا است. نه بالایی وجود دارد و نه پایینی . کبوتر و توکا هر دو اعتراض داشتند. –”صفر ” یعنی چه ؟ مگر “صفر” به معنای “هیچ” نیست؟ چیزی که “هیچ” است، یعنی وجود ندارد. مگر می شود داوری خود را بر پایه “چیزی” بگذاریم که وجود ندارد؟ - سکوت! هر سه نفر رو به من کردند. می خواستند مشکل آنها را حل کنم . پرسیدم: - شماها به چه چیزی “واقعی”می گویید؟ از کجا بفهمیم” چه چیزی وجود دارد و چه چیزی وجود ندارد”؟ کبوتر: - چیزی “وجود دارد” که قابل لمس باشد، بتوان آن را “حس کرد، “وجودی” مادی باشد یا بشود آن را “شنید” یا “بویید”. “صفر ” نه قابل لمس است، نه قابل شنیدن و نه قابل بوییدن.

[sajadhoosein]

یک کاغذ را چند بار می توان تا کرد؟



این مسیله را همه ما تجربه کرده ایم اما شاید هیچ کدام از ما به طور جدی روی آن فکر نکرده باشیم.
اگر ورق را هر بار طوری تا کنید که اندازه آن نصف شود بیش از ۷ یا ۸ بار نمی توانید آن را تا کنید. مهم نیست ورق اولیه شما چقدر بزرگ باشد. شاید تا به حال این قضیه را شنیده باشید و سعی کرده باشید که آن را امتحان کنید و متوجه شده باشید که تا کردن کاغذ بیش از۷ یا ۸ بار بسیار سخت است. آیا می توان گفت که این اعداد یک محدودیت مستدل و عمومی برای تا کردن کاغذ هستند؟
فرض کنید شما کاغذی را انتخاب کرده اید که دارای پهنای w و ضخامت t است . اگر شما شروع به تا کردن ورق از یک سمت بکنید وقتی به جایی برسید که دیگر نتوانید کاغذ را تا کنید یک نوار باریک خواهید داشت.
با هر تا کردن ضخامت کاغذ دو برابر می شود و پهنای آن نصف خواهد شد. یعنی بعد از N بار تا کردن ضخامت ۲n خواهد بود و البته مشخص است که پهنا ۰.۵n می شود
اگر با کاغذی به پهنای ۱۱cm و ضخامت ۰.۰۰۲cm این کار را انجام دهید بعد از ۷ بار تا کردن نسبت t/w برابر ۱/۶ می شود. این بدان معنیست که اندازه ضخامت از پهنا بیشتر می شود و در نتیجه دیگر قادر به تا کردن کاغذ نخواهید بود. اگر این کاغذ را ۵۰ بار بزرگتر کنید شاید بتوانید آن را تا ۱۰ بار هم تا کنید.
اگر به صورت متناوب کاغذ را از عرض و طول تا کنید ممکن است تعداد دفعات بیشتری بتوانید به تا کردن کاغذ ادامه دهید. در این صورت هر بارضخامت دو برابر می شود در صورتی که پهنا هر دو دفعه یک بار نصف می شود.
چندین سال پیش هنگامی که بریتنی گالیوان در دبیرستان درس می خواند با این مسیله رو به رو شد که چگونه کاغذی را ۱۲ بار تا کند . او باید برای گرفتن نمره از یکی از کلاسهایش این مسیله را حل می کرد. بعد از آزمایش راه های مختلف او موفق شد که ورقه نازکی از طلا را ۱۲ بار تا کند. اما مسیله طرح شده در باره کاغذ بود و نه طلا.
گالیوان بر روی معادله تعداد دفعاتی که می توان یک کاغذ با اندازه معین را تا کرد کار کرد.
که در آن L کمترین درازای کاغذ، t میزان ضخامت کاغذ و n تعداد دفعاتی است که می توان کاغذ را تا کرد. واحد t و L باید یکسان باشد.
برای یک طول و ضخامت معین عبارت *******بیانگر آن است که صفحه بعد از n بار تا کردن چند برابر کوچک شده است. با n=۰ شروع می کنیم و به همین ترتیب به رشته ای از اعداد به این صورت می رسیم:
۰, ۱, ۴, ۱۴, ۵۰, ۱۸۶, ۷۱۴, ۲۷۹۴, ۱۱۰۵۰, ۴۳۹۴۶, ۱۷۵۲۷۴, ۷۰۰۰۷۴, ۲۷۹۸۲۵۰, . . .
این به این معنی است که در تای دوازدهم ۲۷۹۸۲۵۰ برابر مقدار کاغذی که در تای اول از دست می رود از دست خواهد رفت.
گالیوان در کتابی با نام ((Historical Society of Pomona Valley)) چگونگی به دست آوردن این معادله و تلاشش برای حل مشکل را توضیح داده است. بالاخره در June ۲۰۰۲ گالیوان یک کاغذ بزرگ را ۱۲بار تا کرد.
راستی اگر از دید دیگری مسیله را نگاه کنیم باز هم جالب خواهد بود. منظورم این است که اگر تا کردن کاغذ را با ارتفاع بسنجیم بعد از ۱۰ بار تا کردن ضخامت کاغذ بدست آمده ۱۰۲۴ برابر حالت اولیه می شود و در مرحله ۱۱ ام۲۰۴۸ و در مرحله ۱۲ ام ۴۰۹۶
یعنی در مرحله دوازدهم باید ۴۰۹۶ برگ را تا کنیم که ضخامتی برابر با حدود ۵۰ سانتی متر که کار خیلی دشوار و تقریبا ناممکن است.

[sajadhoosein]

تصاعد !!



در کشور ما ایران در سده های چهارم و پنجم هجری ، بسیاری از ریاضی دانان ایرانی ، به بررسی تصاعد ها پرداخته‌ اند از جمله « ابوریحان بیرونی » در کتاب خود به نام « آثار الباقیه عن القرون الخالیه » مسیله معروف صفحه شطرنج را که در واقع مسیله ای مربوط به یک تصاعد هندسی است که جمله ی اول آن واحد و تعداد جمله ها ۶۴ باشد ، حل کرده است و با استدلال دقیق ، مجموع جمله های این تصاعد را به دست آورده است
۱۸۴۴۶۷۴۴۰۷۳۵۵۱۶۱۵
درباره صفحه شطرنج ، روایتی وجود دارد . وقتی مخترع شطرنج ، کشف خود را به شاه عرضه کرد ، شاه از اوخواست پاداشی بخواهد ، دانشمند پاسخ داد : به خاطر خانه اول شطرنج ، یک دانه گندم به من بدهید و به خاطر خانه دوم دو دانه‌ی گندم و به خاطر خانه سوم چهار دانه‌ی گندم و همینطور برای هر خانه دو برابر خانه‌ی پیش از آن گندم به من بدهید تا به خانه شصت و چهارم برسد . شاه با ساده لوحی فرمان داد یک کیسه گندم به این مرد بدهید . ولی او نپذیرفت و تقاضا کرد پس از محاسبه دقیق ، گندم را به او بدهند و پس از محاسبه، عددی را که در بالا آوردیم پیدا شد .که اگردر تمام سطح کره زمین (یعنی هر جا که خشکی باشد ) گندم بکارند این مقذار گندم به دست نمی آید. ابوریحان بیرونی با استدلال به این نتیجه رسید که مقدار گندم ها برابر ۲۶۴-۱ و برای محسوس کردن این عدد می گوید:در سطح کره مین ۲۳۰۵ کوه را در نظر می گیریم ، اگر از هر کوه ۱۰۰۰۰رود جاری شود ، در طول رود خانه ۱۰۰۰قطار قاطر حرکت کند و هرقطار شامل ۱۰۰۰قاطر باشد و بر هر قاطر ۸ کیسه گندم قرار داده باشیم . ودر هر کیسه ۱۰۰۰۰دانه گندم باشد . آن وقت عدد همه‌ی این گندم ها از تعداد گندم های صفحه شطرنج کوچکترمی شود.
به نظر شما جالب نیست؟

[sajadhoosein]

منطق فازى



از آن زمان که انسان اندیشیدن را آغاز کرد، همواره کلمات و عباراتى را بر زبان جارى ساخته که مرزهاى روشنى نداشته اند. کلماتى نظیر «خوب»، «بد»، «جوان»، «پیر»، «بلند»، «کوتاه»، «قوى»، «ضعیف»، «گرم»، «سرد»، «خوشحال»، «باهوش»، «زیبا» و قیودى از قبیل «معمولاً»، «غالباً»، «تقریباً» و «به ندرت». روشن است که نمى توان براى این کلمات رمز مشخصى یافت، براى مثال در گزاره «على باهوش است» یا «گل رز زیباست» نمى توان مرز مشخصى براى «باهوش بودن» و «زیبا بودن» در نظر گرفت. اما در بسیارى از علوم نظیر ریاضیات و منطق، فرض بر این است که مرزها و محدوده هاى دقیقاً تعریف شده اى وجود دارد و یک موضوع خاص یا در محدوده آن مرز مى گنجد یا نمى گنجد. مواردى چون همه یا هیچ، فانى یا غیرفانى، زنده یا مرده، مرد یا زن، سفید یا سیاه، صفر یا یک، یا «این» یا «نقیض این» . در این علوم هر گزاره اى یا درست است یا نادرست، پدیده هاى واقعى یا «سفید» هستند یا «سیاه» .
این باور به سیاه و سفیدها، صفر و یک ها و این نظام دو ارزشى به گذشته بازمى گردد و حداقل به یونان قدیم و ارسطو مى رسد. البته قبل از ارسطو نوعى ذهنیت فلسفى وجود داشت که به ایمان دودویى با شک و تردید مى نگریست. بودا در هند، پنج قرن قبل از مسیح و تقریباً دو قرن قبل از ارسطو زندگى مى کرد. اولین قدم در سیستم اعتقادى او گریز از جهان سیاه و سفید و برداشتن این حجاب دوارزشى بود. نگریستن به جهان به صورتى که هست. از دید بودا جهان را باید سراسر تناقض دید، جهانى که چیزها و ناچیزها در آن وجود دارد. در آن گل هاى رز هم سرخ هستند و هم غیرسرخ. در منطق بودا هم A داریم هم نقیض A. در منطق ارسطو یا A داریم یا نقیض A منطق (A یا نقیض A) در مقابل منطق (A و نقیض A). منطق این یا آن ارسطو در مقابل منطق تضاد بودا.
منطق ارسطو اساس ریاضیات کلاسیک را تشکیل مى دهد. براساس اصول و مبانى این منطق همه چیز تنها مشمول یک قاعده ثابت مى شود که به موجب آن یا آن چیز درست است یا نادرست. دانشمندان نیز بر همین اساس به تحلیل دنیاى خود مى پرداختند. گرچه آنها همیشه مطمین نبودند که چه چیزى درست است و چه چیزى نادرست و گرچه درباره درستى یا نادرستى یک پدیده مشخص ممکن بود دچار تردید شوند، ولى در یک مورد هیچ تردیدى نداشتند و آن اینکه هر پدیده اى یا «درست» است یا «نادرست».
هر گزاره، قانون و قاعده اى یا قابل استناد است یا نیست. بیش از دو هزار سال است که قانون ارسطو تعیین مى کند که از نظر فلسفى چه چیز درست است و چه چیز نادرست. این قانون «اندیشیدن» در زبان، آموزش و افکار ما رسوخ کرده است.
منطق ارسطویى دقت را فداى سهولت مى کند. نتایج منطق ارسطویى، «دوارزشى»، «درست یا نادرست»، «سیاه یا سفید» و «صفر یا یک» مى تواند مطالب ریاضى و پردازش رایانه اى را ساده کند. مى توان با رشته اى از صفر و یک ها بسیار ساده تر از کسرها کار کرد. اما حالت دوارزشى نیازمند انطباق ورزى و از بین بردن زواید است. به عنوان مثال هنگامى که مى پرسید: آیا شما از کار خود راضى هستید؟ نمى توان انتظار جواب بله یا خیر داشت، مگر آنکه با تقریب بالایى صحبت کنید. «سورن کیرکگارد» فیلسوف اگزیستانسیالیست، در سال ۱۸۴۳ کتابى در رابطه با تصمیم گیرى و آزاد اندیشى به نام «یا این یا آن» نوشت. او در این کتاب بشر را برده کیهانى انتخاب هاى «دودویى» در تصمیم گیرى هایش نامید. تصمیم گیرى به انجام یا عدم انجام کارى و تصمیم گیرى درباره بودن یا نبودن چیزى.
گرچه مى توان مثال هاى فراوانى را ذکر کرد که کاربرد منطق ارسطویى در مورد آنها صحیح باشد، اما باید توجه داشت که نباید آنچه را که تنها براى موارد خاص مصداق دارد به تمام پدیده ها تعمیم داد. در دنیایى که ما در آن زندگى مى کنیم، اکثر چیزهایى که درست به نظر مى رسند، «نسبتاً» درست هستند و در مورد صحت و سقم پدیده هاى واقعى همواره درجاتى از «عدم قطعیت» صدق مى کند. به عبارت دیگر پدیده هاى واقعى تنها سیاه یا تنها سفید نیستند، بلکه تا اندازه اى «خاکسترى» هستند. پدیده هاى واقعى همواره «فازى»، «مبهم» و «غیردقیق» هستند. تنها ریاضى بود که سیاه و سفید بود. این خود چیزى جز یک سیستم مصنوعى متشکل از قواعد و نشانه ها نبود. علم واقعیت هاى خاکسترى یا فازى را با ابزار سیاه و سفید ریاضى به نمایش مى گذاشت و این چنین بود که به نظر مى رسید واقعیت ها نیز تنها سیاه یا سفید هستند. بدین ترتیب در حالى که در تمامى جهان حتى یک پدیده را نمى توان یافت که صددرصد درست یا صددرصد نادرست باشد، علم با ابزار ریاضى خود همه پدیده هاى جهان را این طور بیان مى کرد. در این جا بود که علم دچار اشتباه شد. در منطق ارسطویى حالت میانه اى وجود ندارد و شیوه استدلال «قطعى و صریح» است. از طرف دیگر ریاضیات فازى بر پایه استدلال تقریبى بنا شده که منطبق با طبیعت و سرشت سیستم هاى انسانى است. در این نوع استدلال، حالت هاى صفر و یک تنها مرزهاى استدلال را بیان مى کنند و در واقع استدلال تقریبى حالت تعمیم یافته استدلال قطعى و صریح ارسطویى است.
در سال ۱۹۶۵، دکتر لطفی‌زاده نظریه سیستم‌های فازی را معرفی کرد. در فضایی که دانشمندان علوم مهندسی به دنبال روش‌های ریاضی برای شکست دادن مسایل دشوارتر بودند، نظریه فازی به گونه‌ای دیگر از مدل‌سازی، اقدام کرد.
منطق فازى، یک جهان بینى جدید است که به رغم ریشه داشتن در فرهنگ مشرق زمین با نیازهاى دنیاى پیچیده امروز بسیار سازگارتر از منطق ارسطویى است. منطق فازى جهان را آن طور که هست به تصویر مى کشد. بدیهى است چون ذهن ما با منطق ارسطویى پرورش یافته، براى درک مفاهیم فازى در ابتدا باید کمى تامل کنیم، ولى وقتى آن را شناختیم، دیگر نمى توانیم به سادگى آن را فراموش کنیم. دنیایى که ما در آن زندگى مى کنیم، دنیاى مبهمات و عدم قطعیت است. مغز انسان عادت کرده است که در چنین محیطى فکر کند و تصمیم بگیرد و این قابلیت مغز که مى تواند با استفاده از داده هاى نادقیق و کیفى به یادگیرى و نتیجه گیرى بپردازد، در مقابل منطق ارسطویى که لازمه آن داده هاى دقیق و کمى است، قابل تامل است.

[sajadhoosein]

کاربرد مثلث در موسیقی



مثلث از ابتدایی ترین اشکال هندسی بوده که انسانها در هنر از آن استفاده میکردند، بدون شک اولین نوع از انواع مثلث هم که در هنر از آن استفاده شده مثلث متساول الاضلاع بوده است. اهرام مصر نمونه بسیاری قدیمی (حدود ۲۸۰۰ سال پیش از میلاد) از کاربری مثلت در هنر معماری قدیم بوده است. نمونه های دیگر از استفاده از مثلث در هنر تمدن های قدیم را می تواند در کاشی کاری های دیواره معابد در نپال نیز مشاهده کرد.
معروف هست تالس (۶۴۰-۵۵۰ سال پیش از میلاد) که پدر ریاضیات، نجوم و فلسفه یونان باستان بوده از شاگردان خود می خواهد که به مصر سفر کنند تا از پیشرفت علوم در آن تمدن اطلاعات لازم را کسب کنند و فیثاغورث (Pythagoras) از اولین افرادی بوده که این دستور را می پذیرد و به مصر سفر میکند. فیثاغورث از بنیانگذاران علمی موسیقی در جهان بوده و اغلب از هندسه برای مدل کردن استفاده می کرده، می خواهیم با استفاده از تجربیات او سلسه مطالبی را پیرامون ارتباط موسیقی با علوم هندسه، فیزیک و ریاضی آغاز کنیم.
موسیقی را می توانیم به روشهای مختلف مدل کنیم برای شروع کار ساده ترین روش را انتخاب میکنم که عبارت است از مدل کردن عمودی موسیقی یاهمان هارمونی. این روش مدل کردن به موسیقیدان ها کمک می کند تا هنگام فکر یا گوش کردن به هارمونی تصویر بهتری از نت های موسیقی داشته باشند بخصوص برای نوازندگان سازغیر از پیانو.
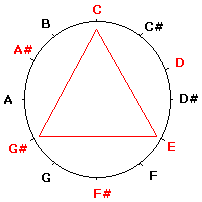
یک دایره در نظر بگیرید و آنرا به دوازده قسمت مساوی (یک اکتاو کروماتیک) تقسیم کنید و نت ها را به ترتیب روی هر قسمت بنویسد مانند شکل. یکی از ساده ترین اشکال هندسی که در این دایره تقسیم شده می توان ساخت مثلت متساوی الاضلاع می باشد. که اگر آنرا بسازید و به آن دقت کنید تفسیر موسیقی آن یک آکورد افزوده خواهد بود. حتما” شنید که آکوردهای افزوده جدای از اینکه معکوس باشند یا نه چهار حالت بیشتر نیستند که دایره فوق این موضوع را بسادگی نمایش میدهد چرا که اگر راس بالایی مثلث را در جهت عقربه های ساعت حرکت دهیم تا رسیدن به نت E و انطباق دوباره روی خود، می تواند سه حالت دیگر را به خود بگیرد. همچنین به وضوح در شکل می توان دید که یک آکورد افزوده از سه فاصله (که در اینجا هرکدام یک ضلع مثلث هستند) یکسان معادل ۴ نیم پرده تشکیل شده است.

مثلث متساول الاضلاع معادل یک آکورد افزوده

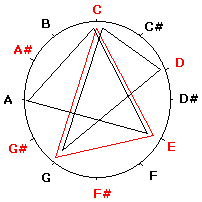
شما باز هم می توانید مثلث های دیگری درست کنید. به شکل بعدی نگاه کنید که آکوردهای دو ماژور و لا مینور را نمایش میدهد. این دو مثلث (آکورد) خصوصیات جالبی دارند اولا” اضلاع آنها باهم برابر است، ثانیا” نسبت به خطی که از D کشیده میشود و به G# خطم میشود متقارن می باشند، حتما” می دانید که مینور نسبی گام دو ماژور، لامینور می باشد. به این طریق شما می توانید یک روش ساده برای پیدا کردن گامهای مینور و ماژور نسبی پیدا کنید، هر چند اینکار در پیانو بخاطر وضوح دیداری که چیدمان نت ها وجود دارد ساده می باشد.
مثلث های متساوی الساقین هم جالب هستند یکی از آنها آکورد sus۲ را تشکیل میدهد که در شکل مشاهده میکنید و همچنین میتوانید آکوردهای کاسته را نیز باز با یک مثلث متساوی الساقین درست کنید. اگر دقت کنید این مثلث متساوی الساقین حالت آکورد sus۲ برای C و حالت آکورد sus۴ برای G دارد. بنابراین می توان به ارتباط نزدیک آکوردهای sus> در حالت های ۲ و ۴ برای فاصله های پنجم با یکدیگر پی برد. این نکته هم جالب خواهد بود اگر شما راس D در این مثلث را نسبت به راس C قرینه کنید به آکورد sus۲ دیگری می رسید که یک پرده عقب تر است آکورد Csus۴قرار دارد.

آکوردهای بزرگ، کوچک، sus۲ و sus۴

شما می توانید دامنه مدل کردن را ادامه دهید و راجع به سایر مثلث ها فکر کنید، همچنین می توانید آکوردهای چهار صدایی را با انواع چهار ضلعی ها مدل کنید. سیوالی که پیش می آید این است که آیا هستند افرادی که با شنیدن موسیقی این اشکال در ذهن آنها نقش ببندد؟

[sajadhoosein]

اعداد اول
تعریف: عدد طبیعی p>1,pرا اول می نامند به شرطی که تنها مقسوم علیه های مثبت آن 1وp باشند. اگرعددی طبیعی وبزرگتر از 1 اول نباشد مرکب است.

قضیه 1: تعداد اعداد اول نامتناهی است.
آیا می توانید اثبات کنید که بینهایت عدد اول داریم؟
برهان: اول از همه باید بدانیم که اعداد طبیعی که تعداد آنها بینهایت است یا عددیاول هستند و یا اینکه حاصل ضربی از اعداد اول می باشند و از این دو حالت خارج نیست. حالا می خواهیم اثبات کنیم که تعداد اعداد اول بینهایت است. برای این کار ازبرهان خلف استفاده می کنیم یعنی فرض می کنیم اعداد اول متناهی هستند.حالا فرض می کنیم اعداد اولی که گفتیم تعداد آنها بینهایت نیست عبارتند از:P1وP2وP3و.....وPn
همان طور که قبلا گفتیم اعداد طبیعی یا عددی اول هستند و یا اینکه حاصل ضربیاز اعداد اول می باشند(غیراز عددیک) و از این دو حالت خارج نیست و به عبارتیحاصل ضرب همه اعداد اول فرض شده ی بالا به اضافه ی یک بر هیچ یک از اون اعداداول بخشپذیر نیست و این ممکن نیست که عددی وجود داشته باشد که نه اول باشد ونه حاصل ضربی از اعداد اول و به عبارتی به یک چیز نا ممکن رسیدیم، پس فرضمسئله اشتباه است و به عبارتی بینهایت عدد اول داریم.
خلاصه بحث: حکم را به روشی که منسوب به اقلیدس است اثبات می کنیم: فرض کنیدتعداد اعداد اول متناهی و تعداد آنها n تا باشد . حال عدد M را که برابرحاصلضرب این اعداد به علاوه ی 1 را در نظر بگیرید. این عدد مقسوم علیهی غیراز آن n عدد دارد که با فرض در تناقض است.(البته شایان ذکر است که این قضیه اثبات های گوناگونی دارد که ما ساده ترینآنها را انتخاب کردیم اگر مایلید می توانید اثبات های دیگر آن را بیاورید).

قضیه 2:قضیه ی اساسی حساب: هر عدد طبیعی بزرگتر از 1 را به شکل حاصلضرباعدادی اول نوشت.

قضیه 3: قضیه چپیشف: اگر n عددی طبیعی و بزرگتر از 2 باشد, حتما" بین n و 2n عدد اولی وجود دارد.

حدس گلدباخ

انگاره‌ی گلدباخ (حدس گلدباخ) از جمله معروف‌ترین مسایل حل نشده‌ی ریاضیات می‌باشد. برای درک این مساله تنها کافیست با مفهوم اعداد اول آشنا باشید. این انگارهچنین است:

هر عدد صحیح زوج بزرگ‌تر از 2 حاصل‌جمع دو عدد اول است.
صورت معادل آن چنین است:
هر عدد صحیح زوج بزرگ‌تر از 5 حاصل‌جمع سه عدد اول است.

تاریخچه
گلدباخ (1690 – 1764) به خاطر این حدس که آن را در سال 1742 در نامه‌ای به اویلرمطرح کرد، نامش در تاریخ ریاضیات باقی مانده است. او ملاحظه کرد در هر موردی کهامتحان می‌کند، هر عدد زوج را (به جز 2 و 5) می‌توان به صورت مجموع سه عدد اولنوشت.اویلر حدس گلدباخ را تعمیم داد به طوری‌که هر عدد زوج بزرگ‌تر از 2 را می‌توانبه صورت مجموع دو عدد اول نوشت. مثلاً:

4=2+2 , 6=3+3 , 8=5+3 , 10=5+5 , 12=5+7 , 14=7+7 , 16=13+3 , 18=11+7 , 20=13+7 ,
… , 48 = 29 +19 , … , 100 = 97 + 3 , …

گلدباخ از اویلر پرسید که آیا می‌تواند این مطلب را برای همه عددهای زوج ثابت کند ویا اینکه مثال نقضی برای آن بیابد؟ شواهد تجربی در تایید اینکه هر عدد زوج به اینصورت قابل نمایش است، کاملاً قانع‌کننده است و هر کسی می‌تواند با امتحان کردن چندعدد زوج، این موضوع را تحقیق کند. منشأ دشواری در این است که عددهای اول بر حسب ضربتعریف می‌شوند در حالی که این مسأله با جمع سروکار دارد. به طور کلی، اثبات رابطهبین ویژگیهای ضربی و جمعی اعداد صحیح کار مشکلی است.

تلاش‌ها برای اثبات
در سال 1931 اشنیرلمان (1905-1938) که در آن موقع یک ریاضیدان روس جوان و گمنامبود موفقیت مهمی در این زمینه به دست آورد که برای همه متخصصان غیرمنتظره وشگفت‌آور بود. او ثابت کرد هر عدد صحیح مثبت را می‌توان به صورت مجموع حداکثر 300000 عدد اول نمایش داد. گر چه این نتیجه در مقایسه با هدف اصلی یعنی اثباتانگاره‌ی گلدباخ مضحک به نظر می‌رسد، ولی این نخستین گام در آن جهت بود. ایناثبات مستقیم و سازنده است، اما هیچ روش خاصی برای تجزیه یک عدد صحیح دلخواه بهاعداد اول ارائه نمی‌کند.
بعدا وینوگرادوف ریاضیدان روس با استفاده از روشهای هاردی ، لیتلوود و همکار هندیبرجسته آنها رامانوجان در نظریه تحلیلی اعداد ، موفق شد تعداد عددهای اول موردلزوم را از 300000 به 4 کاهش دهد. این نتیجه به تعداد مطلوب در انگاره گلدباخبسیار نزدیکتر است ولی تفاوت عمده‌ای بین حکم اشنیرلمان و حکم وینوگرادوف وجوددارد که شاید مهمتر از اختلاف میان 300000 و 4 باشد. قضیه وینوگرادوف فقط به ازایهمه اعداد صحیح «به اندازه کافی بزرگ» ثابت شده است؛ به بیان دقیقتر، او ثابت کردعدد صحیح N ای وجود دارد به طوری که هر عدد صحیح n>N را می‌توان به شکل مجموعحداکثر 4 عدد اول نشان داد. اثبات وینوگرادوف راهی برای براورد کردن N به ما نشاننمی‌دهد، و بر خلاف اثبات اشنیرلمان، اساساً غیرمستقیم و غیرسازنده است. درحقیقت، چیزی که وینوگرادوف ثابت کرد این است که فرض نامتناهی بودن تعداد عددهایصحیحی که قابل تجزیه به حداکثر 4 عدد اول نیستند، به نتیجه نامعقولی می‌انجامد.در اینجا با نمونه خوبی از تفاوت عمیق میان دو نوع اثبات، مستقیم و غیرمستقیم، روبه روییم.
در سال 1956 باروتسکین با نشان دادن اینکه عدد exp(exp(16/038))=n در قضیهوینوگرادف کافیست گام دیگری در این راه نهاد.در 1919 ویگوبرون رویکرد متفاوتی با عنوان روش غربال مطرح کرد که تعمیمی از غربالاراتستن است. او ثابت کرد هر عدد صحیح زوجی که به قدر کافی بزرگ باشد ، مجموع دوعدد است که هر کدام از آنها حاصل‌ضرب حداکثر 9 عدد اول هستند.
در 1937 ریچی ثابت کرد هر عدد زوجی که به قدر کافی بزرگ باشد مجموع دو عدد است کهیکی حاصل‌ ضرب حداکثر دو عدد اول و دیگری حاصل‌ضرب حداکثر 366 عدد اول است.کُن با بهره‌گیری از ایده‌های ترکیبیاتی بوخشتاب ثابت کرد هر عدد زوج بقدر کافیبزرگ مجموع دو عدد است که هر یک حاصل‌ضرب حداکثر چهار عدد اول است.
در 1957 ، ونگ یوان با فرض درست بودن صورت تعمیم یافته فرضیه ریمان ثابت کرد هرعدد صحیح زوج بقدر کافی بزرگ ،‌مجموع یک عدد اول و حاصل‌ضرب حداکثر سه عدد اولاست.
در 1948 آلفرد بدون استفاده از صورت تعمیم یافته فرضیه ریمان ثابت کرد که هر عددزوج بقدر کافی بزرگ مجموع یک عدد اول و حاصل‌ضرب حداکثر c عدد اول است. ( c عددیثابت و مجهول است). در 1961 باربن نشان داد که c=9 برای این منظور کفایت می‌کند.
در 1962 ، پان چنگ دونگ این مقدار را به c=5 کاهش داد. مدت کوتاهی پس از آن باربنو پان ، مستقل از هم ،‌آن را به c=4 کاهش دادند.
در 1965 بوخشتاب این قضیه را به ازای c=3 کاهش داد.
در 1966 ، چن جینگ ران روش غربال را بهتر کرد و قضیه را به ازای c=2 ثابت کرد.یعنیهر عدد صحیح زوجی که به قدر کافی بزرگ باشد ، مجموع یک عدد اول و حاصل‌ضرب حداکثردو عدد اول است.

[sajadhoosein]

خاصیت اعداد بین صفر و یک




در یک عبارت توان مانند a به توان x که a مثبت و ثابت و x عدد بزرگتر از یک باشد حاصل توان نیز زیاد میشود اما اگر a کوچکتر از یک و بزرگتر از صفر باشد (بین صفر و یک) حاصل توان کوچکتر میشود.
به عبارت دیگر برای مثال شما اگر ۲ را به توان سه برسانید میشود هشت که از دو بیشتر است , اما اگر یک دوم )که عددی بین صفر و یک است) را به توان ۳ برسانید می شود یک هشتم که از یک دوم کوچکتر است.این خاصیت اعداد است که اگر عدی در انها ضرب شود یا به توان برسند جوابشان کوچکتر میشود.
* ایا میدانستید که اگر یک عدد دو رقمی را انتخاب کنید(مثل ۴۷ یا ۸۹ و …) و
سپس عددهای ان را از خود عدد دو رقمی کم کنید(مثلا عدد ۴۷ : ۳۶ = ۷ - ۴ - ۴۷ )
عدد بدست امده همیشه مضربی از ۹ خواهد بود.
همچنین در مورد اعداد ۳ رقمی اگر چنین عملی شود
(مثلا ۷۲۳ : ۷۱۱ = ۳ - ۲ - ۷ - ۷۲۳ )حال اگر رقمهای عدد بدست امده را با هم جمع کنید۹ = ۱+۱+۷ همیشه جواب یا ۹ خواهد بود یا ۱۸.
* عدد ۶ به هر توان طبیعی که برسد رقم یکان جوابش ۶ و رقم دهگانش فرد است و رقم یکان نصف این عدد همیشه ۸ خواهد بود.
* ۴ تقسیم بر یک دوم ۸ خواهد بود که به نظر می اید میشود ۲.

[sajadhoosein]

تاریخچه عدد صفر



یکی از معمول ترین سیوالهایی که مطرح می شود این است که: چه کسی صفر را کشف کرد؟ البته برای جواب دادن به این سیوال بدنبال این نیستیم که بگوییم شخص خاصی صفر را ابداع و دیگران از آن زمان به بعد از آن استفاده می کردند.
اولین نکته شایان ذکر در مورد عدد صفر این است که این عدد دو کاربرد دارد که هر دو بسیار مهم تلقی می شود یکی از کاربردهای عدد صفر این است که به عنوان نشانه ای برای جای خالی در دستگاه اعداد (جدول ارزش مکانی اعداد) بکار می رود. بنابراین در عددی مانند ۲۱۰۶ عدد صفر استفاده شده تا جایگاه اعداد در جدول مشخص شود که بطور قطع این عدد با عدد ۲۱۶ کاملاً متفاوت است. دومین کاربرد صفر این است که خودش به عنوان عدد بکار می رود که ما به شکل عدد صفر از آن استفاده می کنیم.
هیچکدام از این کاربردها تاریخچه پیدایش واضحی ندارند. در دوره اولیه تاریخ کاربرد اعداد بیشتر بطور واقعی بوده تا عصر حاضر که اعداد مفهوم انتزاعی دارند. بطور مثال مردم دوران باستان اعداد را برای شمارش تعداد اسبان، … بکار می برند و در اینگونه مسایل هیچگاه به مسیله ای برخورد نمی کردند که جواب آن صفر یا اعداد منفی باشد.
بابلیها تا مدتها در جدول ارزش مکانی هیچ نمادی را برای جای خالی در جدول بکار نمی بردند. می توان گفت از اولین نمادی که آنها برای نشان دادن جای خالی استفاده کردن گیومه (”) بود. مثلاً عدد۶″۲۱ نمایش دهنده ۲۱۰۶ بود. البته باید در نظر داشت که از علایم دیگری نیز برای نشان دادن جای خالی استفاده می شد ولیکن هیچگاه این علایم به عنوان آخرین رقم آورده نمی شدندبلکه همیشه بین دو عدد قرار می گیرند بطور مثال عدد “۲۱۶ را با این نحوه علامت گذاری نداریم. به این ترتیب به این مطلب پی می بریم که کاربرد اولیه عدد صفر برای نشان دادن جای خالی اصلاً به عنوان یک عدد نبوده است.
البته یونانیان هم خود را از اولین کسانی می دانند کهدرجای خالی ,صفر استفاده می کردند اما یونانیان دستگاه اعداد (جدول ارزش مکانی اعداد) مثل بابلیان نداشتند. اساساً دستاوردهای یونانیان در زمینه ریاضی بر مبنای هندسه بوده و به عبارت دیگر نیازی نبوده است که ریاضی دانان یونانی از اعداد نام ببرند زیر آنها اعداد را بعنوان طول خط مورد استفاده قرار می دادند.
البتهبعضى ازریاضی دانان یونانی ثبت اطلاعات نجومی را بر عهده داشتند. در این قسمت به اولین کاربرد علامتی اشاره می کنیم که امروزه آن را به این دلیل که ستاره شناسان یونانی برای اولین بار علامت ۰ را برای آن اتخاذ کردند، عدد صفر می نامیم. تعداد معدودی از ستاره شناسان این علامت را بکار بردند و قبل از اینکه سرانجام عدد صفر جای خود را بدست آورد، دیگر مورد استفاده قرار نگرفت و سپس در ریاضیات هند ظاهر شد.
هندیان کسانی بودند که پیشرفت چشمگیری در اعداد و جدول ارزش مکانی اعداد ایجاد کردند هندیان نیز از صفر برای نشان دادن جای خالی در جدول استفاده می کردند.
اکنون اولین حضور صفر را به عنوان یک عدد مورد بررسی قرار می دهیم اولین نکته ای که می توان به آن اشاره کرد این است که صفر به هیچ وجه نشان دهنده یک عدد بطور معمول نمی باشد. از زمانهای پیش اعداد به مجموعه ای از اشیاء نسبت داده می شدند و در حقیقت با گذشت زمان مفهوم صفر و اعداد منفی که از ویژگیهای مجموعه اشیاء نتیجه نمی شدند، ممکن شد. هنگامیکه فردی تلاش می کند تا صفر و اعداد منفی را بعنوان عدد در نظر بگیرید با این مشکل مواجه می شود که این عدد چگونه در عملیات محاسباتی جمع، تفریق، ضرب و تقسیم عمل می کند. ریاضی دانان هندی سعی بر آن داشتند تا به این سیوالها پاسخ دهندو در این زمینه نیز تا حدودى موفق بوده اند .
این نکته نیز قابل ذکر است که تمدن مایاها که در آمریکای مرکزی زندگی می کردند نیز از دستگاه اعداد استفاده می کردند و برای نشان دادن جای خالی صفر را بکار می برند.
بعدها نظریات ریاضی دانان هندی علاوه بر غرب، به ریاضی دانان اسلامی و عربی نیز انتقال یافت. فیبوناچی، مهمترین رابط بین دستگاه اعداد هندی و عربی و ریاضیات اروپا می باشد.
یکی از معمول ترین سیوالهایی که مطرح می شود این است که: چه کسی صفر را کشف کرد؟ البته برای جواب دادن به این سیوال بدنبال این نیستیم که بگوییم شخص خاصی صفر را ابداع و دیگران از آن زمان به بعد از آن استفاده می کردند.
اولین نکته شایان ذکر در مورد عدد صفر این است که این عدد دو کاربرد دارد که هر دو بسیار مهم تلقی می شود یکی از کاربردهای عدد صفر این است که به عنوان نشانه ای برای جای خالی در دستگاه اعداد (جدول ارزش مکانی اعداد) بکار می رود. بنابراین در عددی مانند ۲۱۰۶ عدد صفر استفاده شده تا جایگاه اعداد در جدول مشخص شود که بطور قطع این عدد با عدد ۲۱۶ کاملاً متفاوت است. دومین کاربرد صفر این است که خودش به عنوان عدد بکار می رود که ما به شکل عدد صفر از آن استفاده می کنیم.
هیچکدام از این کاربردها تاریخچه پیدایش واضحی ندارند. در دوره اولیه تاریخ کاربرد اعداد بیشتر بطور واقعی بوده تا عصر حاضر که اعداد مفهوم انتزاعی دارند. بطور مثال مردم دوران باستان اعداد را برای شمارش تعداد اسبان، … بکار می برند و در اینگونه مسایل هیچگاه به مسیله ای برخورد نمی کردند که جواب آن صفر یا اعداد منفی باشد.
بابلیها تا مدتها در جدول ارزش مکانی هیچ نمادی را برای جای خالی در جدول بکار نمی بردند. می توان گفت از اولین نمادی که آنها برای نشان دادن جای خالی استفاده کردن گیومه (”) بود. مثلاً عدد۶″۲۱ نمایش دهنده ۲۱۰۶ بود. البته باید در نظر داشت که از علایم دیگری نیز برای نشان دادن جای خالی استفاده می شد ولیکن هیچگاه این علایم به عنوان آخرین رقم آورده نمی شدندبلکه همیشه بین دو عدد قرار می گیرند بطور مثال عدد “۲۱۶ را با این نحوه علامت گذاری نداریم. به این ترتیب به این مطلب پی می بریم که کاربرد اولیه عدد صفر برای نشان دادن جای خالی اصلاً به عنوان یک عدد نبوده است.
البته یونانیان هم خود را از اولین کسانی می دانند کهدرجای خالی ,صفر استفاده می کردند اما یونانیان دستگاه اعداد (جدول ارزش مکانی اعداد) مثل بابلیان نداشتند. اساساً دستاوردهای یونانیان در زمینه ریاضی بر مبنای هندسه بوده و به عبارت دیگر نیازی نبوده است که ریاضی دانان یونانی از اعداد نام ببرند زیر آنها اعداد را بعنوان طول خط مورد استفاده قرار می دادند.
البتهبعضى ازریاضی دانان یونانی ثبت اطلاعات نجومی را بر عهده داشتند. در این قسمت به اولین کاربرد علامتی اشاره می کنیم که امروزه آن را به این دلیل که ستاره شناسان یونانی برای اولین بار علامت ۰ را برای آن اتخاذ کردند، عدد صفر می نامیم. تعداد معدودی از ستاره شناسان این علامت را بکار بردند و قبل از اینکه سرانجام عدد صفر جای خود را بدست آورد، دیگر مورد استفاده قرار نگرفت و سپس در ریاضیات هند ظاهر شد.
هندیان کسانی بودند که پیشرفت چشمگیری در اعداد و جدول ارزش مکانی اعداد ایجاد کردند هندیان نیز از صفر برای نشان دادن جای خالی در جدول استفاده می کردند.
اکنون اولین حضور صفر را به عنوان یک عدد مورد بررسی قرار می دهیم اولین نکته ای که می توان به آن اشاره کرد این است که صفر به هیچ وجه نشان دهنده یک عدد بطور معمول نمی باشد. از زمانهای پیش اعداد به مجموعه ای از اشیاء نسبت داده می شدند و در حقیقت با گذشت زمان مفهوم صفر و اعداد منفی که از ویژگیهای مجموعه اشیاء نتیجه نمی شدند، ممکن شد. هنگامیکه فردی تلاش می کند تا صفر و اعداد منفی را بعنوان عدد در نظر بگیرید با این مشکل مواجه می شود که این عدد چگونه در عملیات محاسباتی جمع، تفریق، ضرب و تقسیم عمل می کند. ریاضی دانان هندی سعی بر آن داشتند تا به این سیوالها پاسخ دهندو در این زمینه نیز تا حدودى موفق بوده اند .
این نکته نیز قابل ذکر است که تمدن مایاها که در آمریکای مرکزی زندگی می کردند نیز از دستگاه اعداد استفاده می کردند و برای نشان دادن جای خالی صفر را بکار می برند.
بعدها نظریات ریاضی دانان هندی علاوه بر غرب، به ریاضی دانان اسلامی و عربی نیز انتقال یافت. فیبوناچی، مهمترین رابط بین دستگاه اعداد هندی و عربی و ریاضیات اروپا می باشد.

[sajadhoosein]

عمل سریع ضرب



ضرب اعداد در دوازده:
دستور:هر رقم را دو برابر کن بعد با همسایه اش(رقم سمت راست را همسایه مینامیم) جمع کن.
مثال:
۰۴۱۲*۱۲
۲*۲=۴
۱*۲+۲=۴
۴*۲+۱=۹
۰*۲+۴=۴
جواب:۴۹۴۴
چه راحت!!
عمل سریع ضرب ۱۱
۱) آخرین رقم مضروب (عددی که در یازده ضرب میشود ) را به عنوان رقم سمت راست جواب مینویسیم.
۲)هر عدد مضروب را با همسایه سمت راست آن جمع میکنیم.
۳)و آخرین مرحله کار که اولین رقم مضروب سمت چپ جواب میشود مثال:
۱۱*۵۲۴
دستور اول:
آخرین رقم ۵۲۴ را به عنوان جواب مینویسیم:
۴
دستور دوم:
۴+۲=۶
ادامه:
۲+۵=۷
دستور سوم:
اولین رقم سمت راست مضروب را سمت چپ جواب مینویسیم.
۵
جواب:۵۷۶۴