سلام 2 تا سوال هست که می خواستم بهم در حلشون کمک کنید ( یا با حلش یا با راهنمایی در حلش ) ...
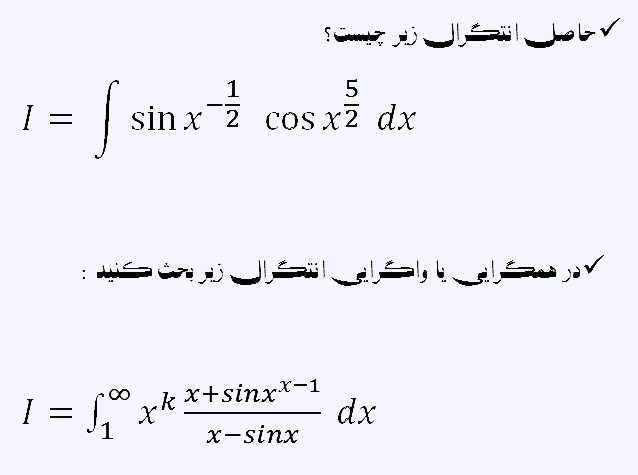
سلام 2 تا سوال هست که می خواستم بهم در حلشون کمک کنید ( یا با حلش یا با راهنمایی در حلش ) ...
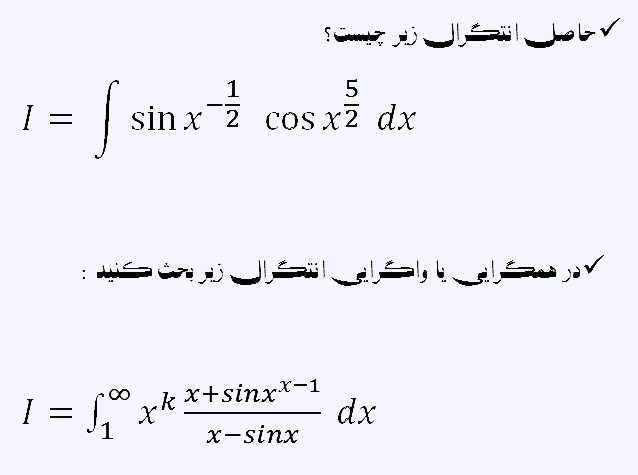

با سلام کسی هست این سوال را حل کنه ؟
مثلث Abc را که دارای زاوایای حاده است در نضر میگیریم نیمساز داخلی زاویه ی ش را رسم می کنیم تا ضلع Bc را د نقطه ی L و دایره ی محیطی مثلث را در نقطه ی N قطع کند . از L عمود هایی بر اضلاع Ab و Ac رسم میکنیم و پای دو عمود راk و M می نامیم . ثابت کنید مساحت چهارضلعی Aknm با مساحت مثلث Abc برابر است.

با سلام کسی هست این سوال را حل کنه ؟
مثلث Abc را که دارای زاوایای حاده است در نضر میگیریم نیمساز داخلی زاویه ی ش را رسم می کنیم تا ضلع Bc را د نقطه ی L و دایره ی محیطی مثلث را در نقطه ی N قطع کند . از L عمود هایی بر اضلاع Ab و Ac رسم میکنیم و پای دو عمود راk و M می نامیم . ثابت کنید مساحت چهارضلعی Aknm با مساحت مثلث Abc برابر است.
دیدی که میشه
Polylogarithm
The polylogarithm (also known as de Jonquière's function) is a special function Lis(z) that is defined by the sum
It is in general not an elementary function, unlike the related logarithm function. The above definition is valid for all complex numbers s and z where |z|< 1. The polylogarithm is defined over a larger range of z than the above definition allows by the process of analytic continuation.
The special case s = 1 involves the ordinary natural logarithm (Li1(z)=-ln(1-z)) while the special cases s = 2 and s = 3 are called the dilogarithm (also referred to as Spence's function) and trilogarithm respectively. The name of the function comes from the fact that it may alternatively be defined as the repeated integral of itself, namely that
Last edited by the dead; 24-12-2007 at 22:16.
باسلام و تشكر،
ممنون از پستت اما...(اين اماش كاررا خراب مي كند)
نكته مهم اينست كه آيا اين انتگرال در محدوده اعداد حقيقي جواب دارد يا خير؟
با اين حساب و بدست آوردن اين جواب خفن، پس جواب حقيقي ندارد؟ok؟
حال يك سوال ديگر:
آيااين انتگرال قابل حل است؟
ممنون
يک چيز مشخصی است که انتگرال اولی در محدوده اعداد حقيقی قابل حل نيست و بايد در COMPLEX حل شودسلام 2 تا سوال هست که می خواستم بهم در حلشون کمک کنید ( یا با حلش یا با راهنمایی در حلش ) ...
حل اين نوع انتگرالها در کتاب رياضيات مهندسی توضيح داده شده
Last edited by the dead; 26-12-2007 at 10:12.
سلام والا یه سوال المپیادی داشتم که نمیدونم که دارم تو جای مناسبی مطرحش ممی کنم یا نه اگه نه ببخشید چون من به این قسمت اشنایی ندارم
سوال=چند نقطه داریم که روی یک خط راست واقع نیستند وروی هریک از انان عددی نوشته شده است اگر خطی راست ازنقاط عبور کند تمامی انان حاصلی برابر صفر دارند ثابت کنید که همه ی نقاط مساوی صفر هستند؟
باور کن اصلا منظور سوال را نفهمیدم برای همین ممکنه جواب اشتباه باشهسلام والا یه سوال المپیادی داشتم که نمیدونم که دارم تو جای مناسبی مطرحش ممی کنم یا نه اگه نه ببخشید چون من به این قسمت اشنایی ندارم
سوال=چند نقطه داریم که روی یک خط راست واقع نیستند وروی هریک از انان عددی نوشته شده است اگر خطی راست ازنقاط عبور کند تمامی انان حاصلی برابر صفر دارند ثابت کنید که همه ی نقاط مساوی صفر هستند؟
اگه درست فهمیده باشم تعدادی نقطه داریم که روی همه انها تعدادی عدد نوشته شده است و هر خط راستی که بکشیم مجموع دو عدد صفر می شود.
بین هر دو نقطه ، حتما یک خط راست می توان کشید. اگر عدد روی نقطه انتخابی اول x باشد باید روی نقطه انتخابی دوم x- باشد تا حاصل صفر شود. چون ممکن است دو نقطه ای که انتخاب می شوند هر دو x باشند پس حاصل 2x می شود که حاصل باید صفر باشد یعنی x=0 پس x- هم صفر است
اصلا فکر نمی کنم که منظور را درست گرفته باشم چون این سوال شبیه المپیادی ها نیست..

فکر کنم جوابش این باشه

هم اکنون 1 کاربر در حال مشاهده این تاپیک میباشد. (0 کاربر عضو شده و 1 مهمان)