بنابراین جواب کل قسمت ب میشه:
بقیه قسمت ها هم استدلالاتی مشابه همین دارن.
--------------------------
و اما جواب قسمت ث) اول میایم و رنگی رو که قراره 4 تا مهره از اون رنگ انتخاب بشه رو انتخاب میکنیم. تعداد حالات انتخاب یک رنگ از مجموع 4 رنگ برابره با:
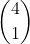
حالا رنگ مورد نظر برای انتخاب 4 مهره از اون رنگ معین شده. چند تا مهره از اون رنگ داریم؟ (جواب: 13 تا) به چند حالت میتونیم 4 تا مهره از مجموع 13 مهره انتخاب کنیم؟ (جواب:
)
حالا میایم و رنگ دوم رو برای انتخاب 2 مهره ی باقیمونده که قراره اون 2 تا هم همرنگ باشند، انتخاب میکنیم. این دفعه 3 تا رنگ باقی موندن. (از رنگی که دفعه ی پیش ازش 4 تا انتخاب کردیم دیگه نمیتونیم مهره برداریم) پس میمونه 3 تا رنگ دیگه. به چند روش میتونیم 1 رنگ رو از مجموع 3 رنگ باقیمونده انتخاب کنیم؟ (جواب:
) باز دوباره میایم و میگیم که این رنگ انتخاب شده چند تا مهره توش داره؟ (جواب: بازم 13 تا) حالا به چند حالت میتونیم 2 مهره از این 13 مهره ی جدید انتخاب کنیم؟ (جواب:
)
مشابه قبل چون همه ی مراحل از هم مستقل بود بنابراین باید تعداد حالات بدست اومده در هر مرحله رو تو هم ضرب کنیم. پس تعداد حالات پیشامد مطلوب ما در قسمت ث برابره با:
و تعداد کل حالات بدون در نظر گرفتن شرط قسمت ث هم که مثل قبل برابره با:
بنابراین احتمال مطلوب در قسمت ث برابره با:
-------------------------------
قسمت ج هم که ساده ترین قسمت کل این سوال هستش. فقط راهنمایی میکنم که از متمم شمارش استفاده کنین. یعنی همه ی حالات منهای اینکه حتی یک مهره ی آبی هم انتخاب نشده باشه. (اصولا هر وقت که تو سوالی کلمه ی
حداقل رو دیدین، به فکر استفاده از متمم بیفتین
.gif "N Aggressive (4)")
)
موفق باشین.
89/9/24
جواب بصورت نقل قول
نوشته شده توسط taghi_ramzi
